दो वृत्तीय कुंडलियां जिनकी त्रिज्याएँ r व R है, को एक समाक्ष रखा गया है एवं केंद्र एक ही है | R>>r के लिएइस व्यवस्था में अन्योन्य प्रेरण का एक व्यंजक ज्ञात कीजिए |
अन्योन्य प्रेरण-"जब दो कुण्डलियों को पास-पास रखकर, उनमे से एक कुण्डली में प्रवाहित धारा के मान में परिवर्तन किया जाता है तो पास रखी से दूसरी कुण्डली में एक प्रेरित वैद्युत वाहक बल उत्पन्न हो जाता है। वैद्युत चुम्बकीय प्रेरण की इस घटना को अन्योन्य प्रेरण कहते हैं।" जिस कुण्डली में धारा परिवर्तित होती है, उसे प्राथमिक कुण्डली तथा जिस कुण्डली में प्रेरित वैद्युत वाहक बल उत्पन्न होता है उसे द्वितीयक कुण्डली कहते हैं। अन्योन्य प्रेरण का उदाहरण ट्रांसफॉर्मर तथा प्रेरण कुण्डली है।
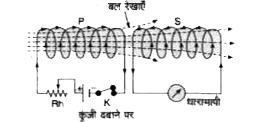
अन्योन्य प्रेरण गुणांक अथवा अन्योन्य प्रेरकत्व-1. माना प्राथमिक कुण्डली में i1 ऐम्पियर की धारा प्रवाहित होने से द्वितीयक कुण्डली के प्रत्येक फेरे से बद्ध चुम्बकीय फ्लक्स ϕ2 है और द्वितीयक कुण्डली में तार के N2 फेरे हैं, अत: द्वितीयक कुण्डली में फ्लक्स ग्रन्थिकाओं की संख्या N2ϕ2 होगी जो कि प्राथमिक कुण्डली में प्रवाहित धारा 1 के अनुक्रमानुपाती होगी।

अतः N2ϕ2∝i1 अथवा N2ϕ2=Mi1
जहाँ म एक नियतांक है, जिसे दोनों कुंडलियों के बिच अन्योन्य प्रेरण गुणांक अथवा अन्योन्य प्रेरकत्व कहते है |
अतः M=N2ϕ2i1
यदि i1=1 ऐम्पियर हो तो M=N2ϕ2, अतः किन्ही दो कुंडलियों के बीचअन्योन्य प्रेरण गुणक अथवा अन्योन्य प्रेरकत्व किसी एक कुंडली में चुम्बकीय फ्लक्स ग्रंथिकाओं की संख्या के बराबर होती है, जबकि निकटवर्ती दूसरी कुंडली में 1 ऐम्पियर धरा प्रवाहित हो रही हो |
2. यदि प्राथमिक कुण्डली में धारा के मान में परिवर्तन करने से द्वितीयक, कुण्डली में प्रेरित वैद्युत वाहक बल e हो तो फैराडे के नियमानुसार,
e2=−N2Δϕ2Δt=−Δ(N2ϕ2)Δt
=−Δ(Mi1)Δt=−M(Δi1Δt)
जहाँ (Δi1/Δt) प्राथमिक कुण्डली में धारा परिवर्तन की दर है। यहाँ पर ऋण चिह्न यह प्रकट करता है कि द्वितीयक कुण्डली में प्रेरित वैद्युत वाहक बल सदैव ऐसी दिशा में उत्पन्न होता है कि वह प्राथमिक कुण्डली में धारा परिवर्तन का विरोध करे |
अतः M=−e2(Δi1/Δt)
यदि Δi1/Δt=1 ऐम्पियर/सेकंड हो तो M=e2 (संख्यात्मक रूप से) |
अत: किन्हीं दो कुण्डलियों के मध्य अन्योन्य प्रेरण गुणांक (अन्योन्य प्रेरकत्व), प्राथमिक कुण्डली में एकांक दर से धारा के परिवर्तित होने पर, द्वितीयक कुण्डली में प्रेरित वैद्युत वाहक बल के संख्यात्मक मान के बराबर होता है।
अन्योन्य प्रेरण गुणांक का मात्रक एवं विमा- इसका मात्रक हेनरी (Henry) तथा विमा [ML2T−2A−2] है |
हेनरी की परिभाषा–यदि प्राथमिक कुण्डली में 1 ऐम्पियर प्रति सेकण्ड की दर से धारा परिवर्तन होने से द्वितीयक कुण्डली में 1 वोल्ट का वैद्युत वाहक बल प्रेरित हो तो दोनों कुण्डलियों के बीच अन्योन्य प्रेरण गुणांक 1 हेनरी होगा। इस प्रकार, 1 हेनरी = 1वॉल्ट 1 ऐम्पियर प्रति सेकंड
अन्योन्य प्रेरण पर क्रोड के पदार्थ का प्रभाव याद कुण्डालया के मध्य लौहचुम्बकीय पदार्थ, जैसे लोहे की क्रोड रख दें अथवा दोनों कुण्डलियों को एक ही क्रोड पर लपेट दें तो द्वितीयक कुण्डली में प्रेरित वैद्युत वाहक बल का मान बढ़ जाएगा जिससे कुण्डलियों में अन्योन्य प्रेरकत्व का मान बढ़ जाएगा ।
दो समतल कुण्डलियों के बीच अन्योन्य प्रेरकत्व-माना R व r(r<<R) त्रिज्या की दो समतल वृत्ताकार कुण्डलियाँ एक-दूसरे के समीप समाक्षीय रूप से (coaxially) रखी हैं। माना त्रिज्या की प्राथमिक कुण्डली में फेरों की संख्या N1 तथा R त्रिज्या की द्वितीयक कुण्डली में फेरों की संख्या Ng है। माना प्राथमिक कुण्डली में i1 ऐम्पियर की धारा प्रवाहित हो रही है।
अतः प्राथमिक कुंडली के केंद्र पर चुम्बकीय क्षेत्र B=μ0N1i12r
माना यह चुम्बकीय क्षेत्र द्वितीयक कुण्डली के सम्पूर्ण तल पर एकसमान है, अतः चुम्बकीय क्षेत्र B के कारण द्वितीयक कुण्डली से बद्ध चुम्बकीय फ्लक्स
अतः कुंडलियों के बीच अन्योन्य प्रेरकत्व M=N2ϕ2i1
=μ0πR2N1N22r
सूत्र से स्पष्ट है कि कुण्डलियों के बीच अन्योन्य प्रेरकत्व M दोनों कुण्डलियों में फेरों की संख्या के अनुक्रमानुपाती होता है। इसके अतिरिक्त अन्योन्य प्रेरकत्व M का मान कुण्डलियों के अन्दर रखे क्रोड पदार्थ पर भी निर्भर करता है। यदि कुण्डलियों के अन्दर नर्म लोहे की छड़ अथवा क्रोड़ रख दी जाए तो अन्योन्य प्रेरकत्व (M) का मान बढ़ जाएगा।
दिया है, N=1000,I=2.5 ऐम्पियर, ϕ=1.4×10−4 वेबर
कुंडली के लिए, Nϕ=LI या L=NϕI
=1000×1.4×10−42.5
=5.6×0−2 हेनरी |
Topper's Solved these Questions
- वैद्युत चुम्बकीय प्रेरणBOOK - UP BOARD PREVIOUS YEARCHAPTER - वैद्युत चुम्बकीय प्रेरणEXERCISE - अतिलघु उत्तरीय प्रश्नोत्तर
25 Videos
- वैद्युत चुम्बकीय प्रेरणBOOK - UP BOARD PREVIOUS YEARCHAPTER - वैद्युत चुम्बकीय प्रेरणEXERCISE - लघु उत्तरीय प्रश्नोत्तर
5 Videos
- वैद्युत आवेश तथा क्षेत्रBOOK - UP BOARD PREVIOUS YEARCHAPTER - वैद्युत आवेश तथा क्षेत्रEXERCISE - विस्तृत उत्तरीय प्रश्नोत्तर
18 Videos
- वैद्युत धारा BOOK - UP BOARD PREVIOUS YEARCHAPTER - वैद्युत धारा EXERCISE - विस्तृत उत्तरीय प्रश्नोत्तर -?
50 Videos
Similar Questions
वैद्युतचुम्बकीय तरंगो का श्रोत क्या है
View Solutionविस्थापन धरा क्या है ? इसका सूत्र लिखिए |
View Solutionएक समान वैद्युत क्षेत्र में स्थित वैद्युत द्विध्रुव पर लगने वाले बल युग्म के आघूर्ण के लिए व्यंजक प्राप्त कीजिए।
अथवा एकसमान वैद्युत क्षेत्र में स्थित वैद्युत द्विध्रुव पर लगने वाला महत्तम बल आघूर्ण का सूत्र प्राप्त कीजिए तथा इसके आधार पर वैद्युत द्विध्रुव आघूर्ण की परिभाषा दीजिए।
View Solutionकिसी चालक तार में प्रवाहित धारा तथा इसमें मुक्त इलेक्ट्रॉनों के अनुगमन वेग से सम्बन्धित व्यंजक का निगमन कीजिए।
View Solutionदो बिंदुओं P और Q के स्थिति सदिश क्रमशः 2¯a+¯b और ¯a−2¯b है। एक बिंदु R का स्थिति सदिश ज्ञात कीजिए जो रेखा खण्ड PQ को 1:2 के अनुपात में अंतः तथा बाहृातः विभाजित करता है।
View Solutionएक अनभिनत पासे को 5 बार उछाला जाता है एक समसंख्या प्राप्त करना एक सफलता है तो प्रायिकता ज्ञात कीजिए - 4 सफलता के लिए
View Solutionएक अनभिनत पासे को 5 बार उछाला जाता है एक समसंख्या प्राप्त करना एक सफलता है तो प्रायिकता ज्ञात कीजिए - अधिक से अधिक 4 सफलताओ के लिए
View Solutionदो वृत्तों, जिनकी त्रिज्याएँ क्रमशः सेमी 1.7 और 2.8 सेमी की है, की एक उभयनिष्ठ तिर्यक स्पर्श रेखा की रचना कीजिए जबकि दोनों के केंद्र एक दूसरे से 6 सेमी दूरी पर है।
View Solutionदो वृत्त जिनकी त्रिज्याएँ क्रमशः 2.5 सेमी एवं 1.5 सेमी है जिनके केंद्र 8 सेमी दूरी पर स्थित है ,पर एक उभयनिष्ठ तिर्यक स्पर्श रेखा किन रचना कीजिए।
View Solutionदो वृत्तों, जिनकी त्रिज्याएँ क्रमशः सेमी 1.7 और 2.8 सेमी की है ,की एक उभयनिष्ठ तिर्यक स्पर्श रेखा की रचना कीजिए जबकि दोनों के केंद्र एक दूसरे से 6 सेमी दूरी पर है।
View Solutionएक सदिश →r, x- अक्ष के साथ 45∘ और y- अक्ष के साथ 60∘ को बनाता है यदि |→r|=10 तो सदिश →r ज्ञात कीजिए।
View Solutionएक दंपत्ति के दो बच्चे है। प्रायिकता ज्ञात कीजिए
दोनों बच्चें लड़कियाँ है , यदि यह ज्ञात है कि बड़ा बच्चा लड़का है।
View Solutionचित्र में दर्शाये अनुसार एक आदर्श गैस के एक मोल को A→B अनुसार लिया गया है। प्रक्रम में निहित कार्य का परिमाण है: (R=253JmolK)
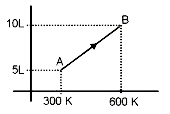
View Solutionविरंजक चूर्ण में इसके एक घटक के रूप में एक ऑक्सोअम्ल का लवण होता है। इस अम्ल का एनहाइड्राइड है:
View Solutionनिम्नलिखित में से कौन सा रेखाचित्र एक समभारिक के लिए है: (दिया गया है: (nR)/P gt 1 )
View Solutionएक एकपरमाण्विक वास्तविक गैस का एक मोल समीकरण p (V — b) = RT को संतुष्ट करता है जहाँ b एक स्थिरांक है। गैस के लिए अंतरापरमाणुक विभव V(r) और अंतरापरमाणुक दूरी r का संबंध निम्नानुसार दर्शाया जाता है
View Solution