The mass of helium atom is 4.0026 amu, while that of the neutron and proton are 1.0087 and 1.0078 amu respectively on the same scale. Hence, the nuclear binding energy per nucleon in the helium atom is about
5 MeV
12 MeV
14 MeV
7 MeV
The correct Answer is:D
To find the nuclear binding energy per nucleon in a helium atom, we will follow these steps:
Step 1: Determine the Mass of the Helium Nucleus
The helium nucleus consists of:
- 2 protons
- 2 neutrons
Given:
- Mass of a proton = 1.0078 amu
- Mass of a neutron = 1.0087 amu
- Mass of helium atom = 4.0026 amu
Step 2: Calculate the Total Mass of Protons and Neutrons
Calculate the total mass of the nucleons (protons and neutrons) in the helium nucleus:
- Total mass of protons = 2 × 1.0078 amu = 2.0156 amu
- Total mass of neutrons = 2 × 1.0087 amu = 2.0174 amu
Now, add these two masses together:
- Total mass of nucleons = Total mass of protons + Total mass of neutrons
- Total mass of nucleons = 2.0156 amu + 2.0174 amu = 4.0330 amu
Step 3: Calculate the Mass Defect
The mass defect (Δm) is the difference between the total mass of the nucleons and the actual mass of the helium atom:
- Δm = Total mass of nucleons - Mass of helium atom
- Δm = 4.0330 amu - 4.0026 amu = 0.0304 amu
Step 4: Calculate the Binding Energy
The binding energy (BE) can be calculated using the mass defect and Einstein's equation, where 1 amu corresponds to approximately 931 MeV:
- Binding Energy (BE) = Δm × 931 MeV
- BE = 0.0304 amu × 931 MeV/amu = 28.3 MeV (approximately)
Step 5: Calculate the Binding Energy per Nucleon
Since there are 4 nucleons in a helium nucleus, we can find the binding energy per nucleon:
- Binding Energy per Nucleon = Total Binding Energy / Number of Nucleons
- Binding Energy per Nucleon = 28.3 MeV / 4 = 7.075 MeV (approximately)
Conclusion
The nuclear binding energy per nucleon in the helium atom is approximately 7 MeV.
---
The helium nucleus consists of:
- 2 protons
- 2 neutrons
- Mass of a proton = 1.0078 amu
- Mass of a neutron = 1.0087 amu
- Mass of helium atom = 4.0026 amu
Calculate the total mass of the nucleons (protons and neutrons) in the helium nucleus:
- Total mass of protons = 2 × 1.0078 amu = 2.0156 amu
- Total mass of neutrons = 2 × 1.0087 amu = 2.0174 amu
- Total mass of nucleons = Total mass of protons + Total mass of neutrons
- Total mass of nucleons = 2.0156 amu + 2.0174 amu = 4.0330 amu
The mass defect (Δm) is the difference between the total mass of the nucleons and the actual mass of the helium atom:
- Δm = Total mass of nucleons - Mass of helium atom
- Δm = 4.0330 amu - 4.0026 amu = 0.0304 amu
The binding energy (BE) can be calculated using the mass defect and Einstein's equation, where 1 amu corresponds to approximately 931 MeV:
- Binding Energy (BE) = Δm × 931 MeV
- BE = 0.0304 amu × 931 MeV/amu = 28.3 MeV (approximately)
Since there are 4 nucleons in a helium nucleus, we can find the binding energy per nucleon:
- Binding Energy per Nucleon = Total Binding Energy / Number of Nucleons
- Binding Energy per Nucleon = 28.3 MeV / 4 = 7.075 MeV (approximately)
The nuclear binding energy per nucleon in the helium atom is approximately 7 MeV.
Topper's Solved these Questions
- NUCLEAR CHEMISTRY Book:ERRORLESS Chapter:NUCLEAR CHEMISTRY Exercise:Ordinary Thinking (Rate of decay and Half - life)
Explore 97 Videos
- NUCLEAR CHEMISTRY Book:ERRORLESS Chapter:NUCLEAR CHEMISTRY Exercise:Ordinary Thinking (Artificial transmutation )
Explore 59 Videos
- NUCLEAR CHEMISTRY Book:ERRORLESS Chapter:NUCLEAR CHEMISTRY Exercise:JEE SECTION (Matrix Match Type Questions)
Explore 2 Videos
- NITROGEN CONTAINING COMPOUNDS Book:ERRORLESS Chapter:NITROGEN CONTAINING COMPOUNDS Exercise:JEE (ADVANCED) 2018 MORE THAN ONE CHOICE CORRECT ANSWER
Explore 1 Video
- ORES, MINERALS AND METALLURGICAL EXTRACTIONBook:ERRORLESS Chapter:ORES, MINERALS AND METALLURGICAL EXTRACTIONExercise:JEE ANSWER TPYE QUESTION (JEE Advanced) 2018) Numeric answer type question
Explore 1 Video
Similar Questions
The atomic mass of F19 is 18.9984 mu. If the masses of proton and neutron are 1.0078mu and .0087mu. Respectively, calculate the binding energy per nucleon (ignore the mass of electrons). (1mu=931)MeV)
View SolutionThe aromic mass of .16O is 15.995 amu while the individual masses of proton and neutron are 1.0073 amu and 1.0087 amu respetively. The mass of electron is 0.000548 amu. Calculate the binding energy of the oxygen nucleus.
View Solution
Knowledge Check
The mass of an atom of 2He4 is 4.0026 amu . The mass of a neutron and a proton are 1.0087 amu and 1.0078 amu respectively. The nuclear binding energy per nucleon is nearly
A7 MeVB5 MeVC10 MeVD14 MeVThe graph between the binding energy per nucleon (E) and atomic mass number (A) is as-
A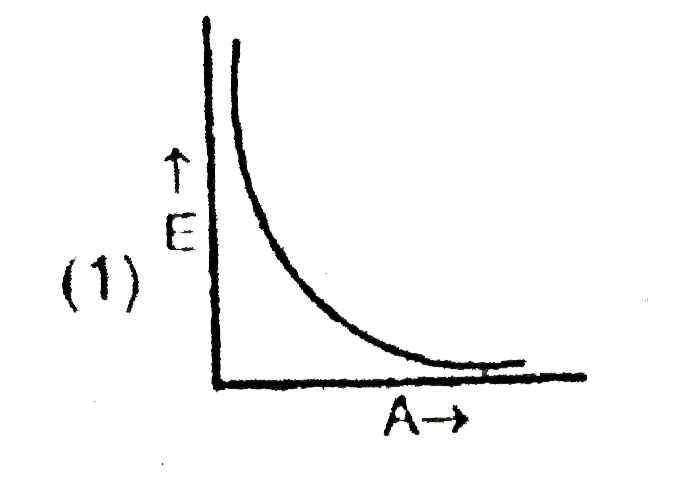 B
B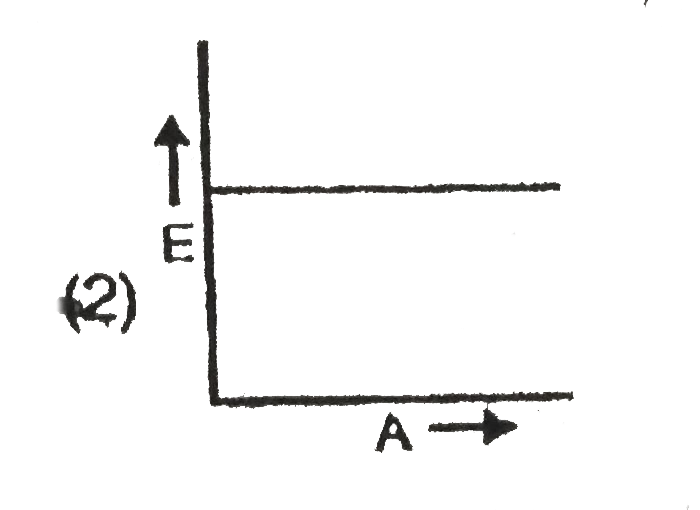 C
C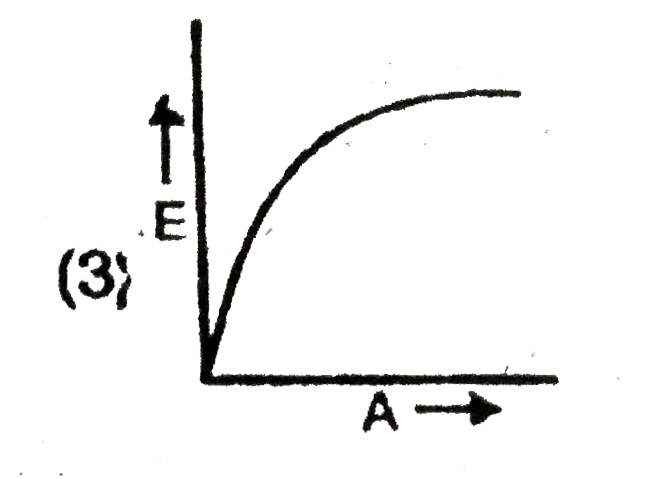 D
D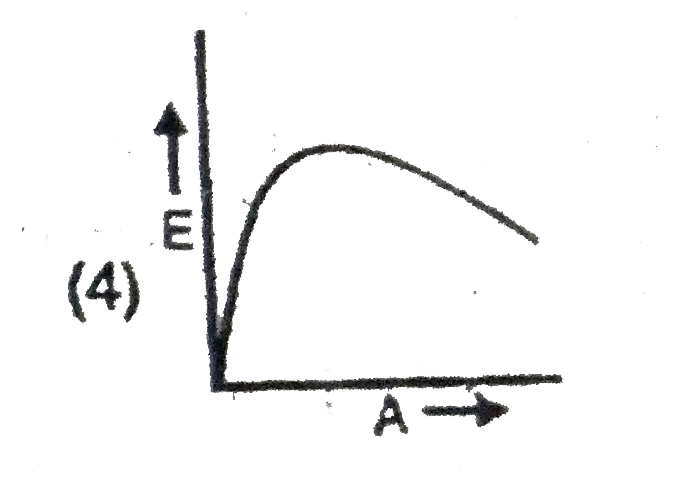
The mass defect of He42 He is 0.03 u. The binding energy per nucleon of helium (in MeV) is
A6.9825B27.93C2.793D69.825
The masses of neutron and proton are 1.0087 a.m.u. and 1.0073 a.m.u. respectively. If the neutrons and protons combine to form a helium nucleus (alpha particles) of mass 4.0015 a.m.u. The binding energy of the helium nucleus will be (1 a.m.u.= 931 MeV)
View SolutionThe masses of neutron and proton are 1.0087 a.m.u. and 1.0073 a.m.u. respectively. If the neutrons and protons combine to form a helium nucleus (alpha particle) of mass 4.0015a.m.u. The binding energy of the helium nucleus will be (1a.m.u.=931MeV).
View SolutionThe mass of .73Li is 0.042 amu less than the sum of masses of its constituents. The binding energy per nucleon is
View SolutionThe nuclear binding energy for Ar (39.962384 amu) is : (given mass of proton and neuron are 1.007825 amu and 1.008665amu respectively)
View SolutionThe mass defect for the nucleus of helium is 0.0303 a.m.u. What is the binding energy per nucleon for helium in MeV ?
View Solution