$._{13} A l^{28}$ when radiated by suitable projectile gives $._{15} P^{31}$ and neutron. The projectile used is

Proton

Neutron

Alpha particle

Deuteron

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:C

To solve the problem, we need to identify the projectile that, when it interacts with aluminum-28, results in the formation of phosphorus-31 and a neutron. Let's break down the steps:
1. Identify the Reaction: The reaction can be represented as:
$_{13}^{28} Al + Projectile \to_{15}^{31} P + n$
where $n$ represents a neutron.
2. Determine the Mass and Atomic Numbers:
- The atomic number of aluminum (Al) is 13, and its mass number is 28.
- The atomic number of phosphorus (P) is 15, and its mass number is 31.
- The neutron has an atomic number of 0 and a mass number of 1.
3. Calculate the Changes in Atomic Number and Mass Number:
- On the left side, the total atomic number is $13 + Z$ (where $Z$ is the atomic number of the projectile).
- The total mass number on the left side is $28 + A$ (where $A$ is the mass number of the projectile).
- On the right side, the total atomic number is $15 + 0 = 15$ (from phosphorus and neutron).
- The total mass number is $31 + 1 = 32$ (from phosphorus and neutron).
4. Set Up the Equations:
- For atomic numbers:
$13 + Z = 15 ⟹ Z = 2$
- For mass numbers:
$28 + A = 32 ⟹ A = 4$
5. Identify the Projectile:
- The atomic number $Z = 2$ corresponds to helium (He), and the mass number $A = 4$ indicates that the projectile is an alpha particle ( $_{2}^{4} He$ ).
6. Conclusion: The projectile used in the reaction is an alpha particle.
Final Answer:
The projectile used is an alpha particle ( $_{2}^{4} He$ ).
---

Updated on:7/8/2024

Class 12 CHEMISTRY CHEMICAL KINETICS

Topper's Solved these Questions

Knowledge Check

When we analyse the projectile motion from any accelerated frame $O$ as ${\to r}_{o}, {\to u}_{o}$ and ${\to a}_{o}$ respectively, express the following terms, ${\to r}_{p O} + {\to a}_{p} - {\to r}_{O}, {\to u}_{p O} = {\to u}_{p} - {\to u}_{O}$ and ${\to a}_{p O} = {\to a}_{p} - {\to a}_{O}$
where $P$ stands for projectile. Then using the following kinematical equations of the projectile (For constant acceleration) relative to the accelerating frame ,we have ${\to S}_{p O} = {\to u}_{p O} t + \frac{1}{2} {\to a}_{p O} t^{2}, {\to v}_{p O}$
$= {\to u}_{p O} + {\to a}_{p O} t$ and $v_{p O}^{2} = u_{p O}^{2} + 2 \to a . {\to s}_{p} O$
Using the above expressions, anwer the following
question:A projectile has initial velocity $v_{0}$ realtive to the large plate which is moving with a constant upward acceleration a.
Refering to Q.1, velocity of the projectile relative to $B$ ofter some time

A $< v_{0} at an angle θ < θ_{0}$
B $> v_{0} at an angle θ > θ_{0}$
C $> v_{0} at an angle θ = θ_{0}$
D $v_{0} at an angle θ = θ_{0}$
When we analyse the projectile motion from any accelerated frame $O$ as ${\to r}_{o}, {\to u}_{o}$ and ${\to a}_{o}$ respectively, express the following terms, ${\to r}_{p O} + {\to a}_{p} - {\to r}_{O}, {\to u}_{p O} = {\to u}_{p} - {\to u}_{O}$ and ${\to a}_{p O} = {\to a}_{p} - {\to a}_{O}$
where $P$ stands for projectile. Then using the following kinematical equations of the projectile (For constant acceleration) relative to the accelerating frame ,we have ${\to S}_{p O} = {\to u}_{p O} t + \frac{1}{2} {\to a}_{p O} t^{2}, {\to v}_{p O}$
$= {\to u}_{p O} + {\to a}_{p O} t$ and $v_{p O}^{2} = u_{p O}^{2} + 2 \to a . {\to s}_{p} O$
Using the above expressions, anwer the following
question:A projectile has initial velocity $v_{0}$ realtive to the large plate which is moving with a constant upward acceleration a.
Which of the following remains equal for the observers $A$ and $B$ ?

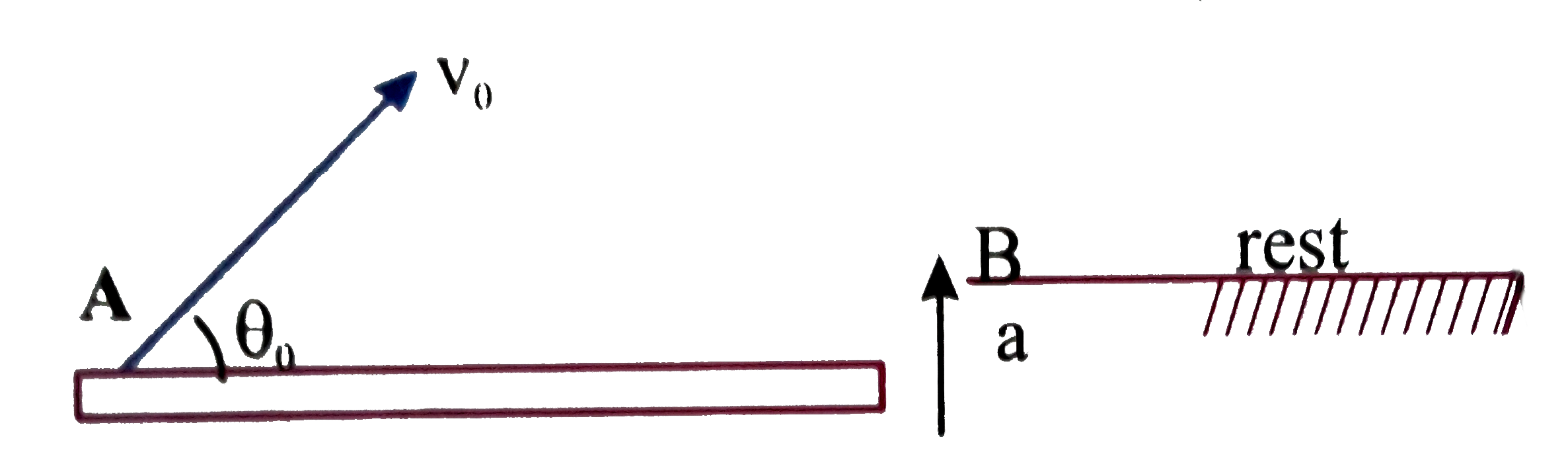AMaximum height
BRange
CTime of flight
DAngle of projection
The highest barrier that a projectile can clear is 13.5 m, when the projectile is launched at an angle of ${15.0}^{\circ}$ above the horizontal. What is the projectile's launch speed?
A15.7 m/s
B62.8 m/s
C44.4 m/s
D22.2 m/s

$._{13} A l^{28}$ when radiated by suitable projectile gives $._{15} P^{31}$ and neutron. The projectile used is

The correct Answer is:C

Topper's Solved these Questions

Similar Questions

Knowledge Check

The highest barrier that a projectile can clear is 13.5 m, when the projectile is launched at an angle of ${15.0}^{\circ}$ above the horizontal. What is the projectile's launch speed?

ERRORLESS -NUCLEAR CHEMISTRY -Ordinary Thinking (Artificial transmutation )

.13Al28 when radiated by suitable projectile gives .15P31 and neutron. The projectile used is

The correct Answer is:C

Topper's Solved these Questions

Similar Questions

Knowledge Check

The highest barrier that a projectile can clear is 13.5 m, when the projectile is launched at an angle of 15.0∘ above the horizontal. What is the projectile's launch speed?

ERRORLESS -NUCLEAR CHEMISTRY -Ordinary Thinking (Artificial transmutation )

$._{13} A l^{28}$ when radiated by suitable projectile gives $._{15} P^{31}$ and neutron. The projectile used is

The highest barrier that a projectile can clear is 13.5 m, when the projectile is launched at an angle of ${15.0}^{\circ}$ above the horizontal. What is the projectile's launch speed?