Given the hypothetical reaction mechanism
AI−−→BII−−→BIII−−→DIV−−→E and the data as

The rate determining step is
Step I
Step II
Step III
Step IV
The correct Answer is:a
The slowest step is the rate determining step . Formation of B(i.e. step I) is the slowest step , therefore , step I is the rate determining step .
Topper's Solved these Questions
- CHEMICAL KINETICS BOOK - ERRORLESS CHAPTER - CHEMICAL KINETICS EXERCISE - Ordinary Thinking (Collision theory , Energy of activation and Arrhenius equation )
45 Videos
- CHEMICAL KINETICS BOOK - ERRORLESS CHAPTER - CHEMICAL KINETICS EXERCISE - Critical Thinking Objective Questions
20 Videos
- CHEMICAL KINETICS BOOK - ERRORLESS CHAPTER - CHEMICAL KINETICS EXERCISE - JEE (Advanced ) 2018
1 Videos
- CHEMICAL EQULIBRIUMBOOK - ERRORLESS CHAPTER - CHEMICAL EQULIBRIUMEXERCISE - JS JEE SECTION (ONLY ONE CHOICE ANSWER (Matrix)
1 Videos
- CHEMISTRY IN EVERYDAY IN LIFEBOOK - ERRORLESS CHAPTER - CHEMISTRY IN EVERYDAY IN LIFEEXERCISE - Critical Thinking (Objective question )
25 Videos
Similar Questions
In the sequence of reaction
AK1−−→BK2−−→CKc−−→D,K3>K2>K1 then the rate determining step of the reaction is
View SolutionFor the following reaction through stages I, II and III AI−−→BII−−→CIII−−→D
quantity of the product formed (x) varies with temperature (T) as given. Select correct statement: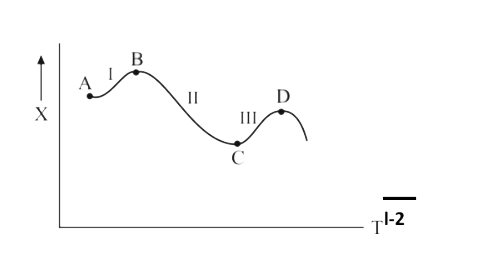
View Solution
Knowledge Check
Given the hypothetical reaction mechanism AI−−→BII−−→CIII−−→DIV−−→E and the rate as

Rate determining step isAstep IBstep IICstep IIIDstep IVGiven the hypothetical reaction mechanism
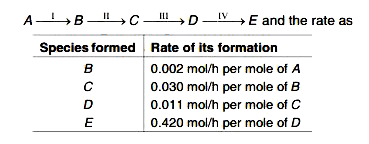 E and the rate as The rate determining step is Astep IBstep IICstep IIIDstep IV
E and the rate as The rate determining step is Astep IBstep IICstep IIIDstep IVLet the vectors →a,→b,→c and →d be such that
(→a×→b)×(→c×→d)=→0. If P1 and P2 are planes determined by the pairs of vectors →a,→b and oerset(→)(c),→d respectively then the angle between P1 and P2 isA0Bπ/4Cπ/3Dπ/2
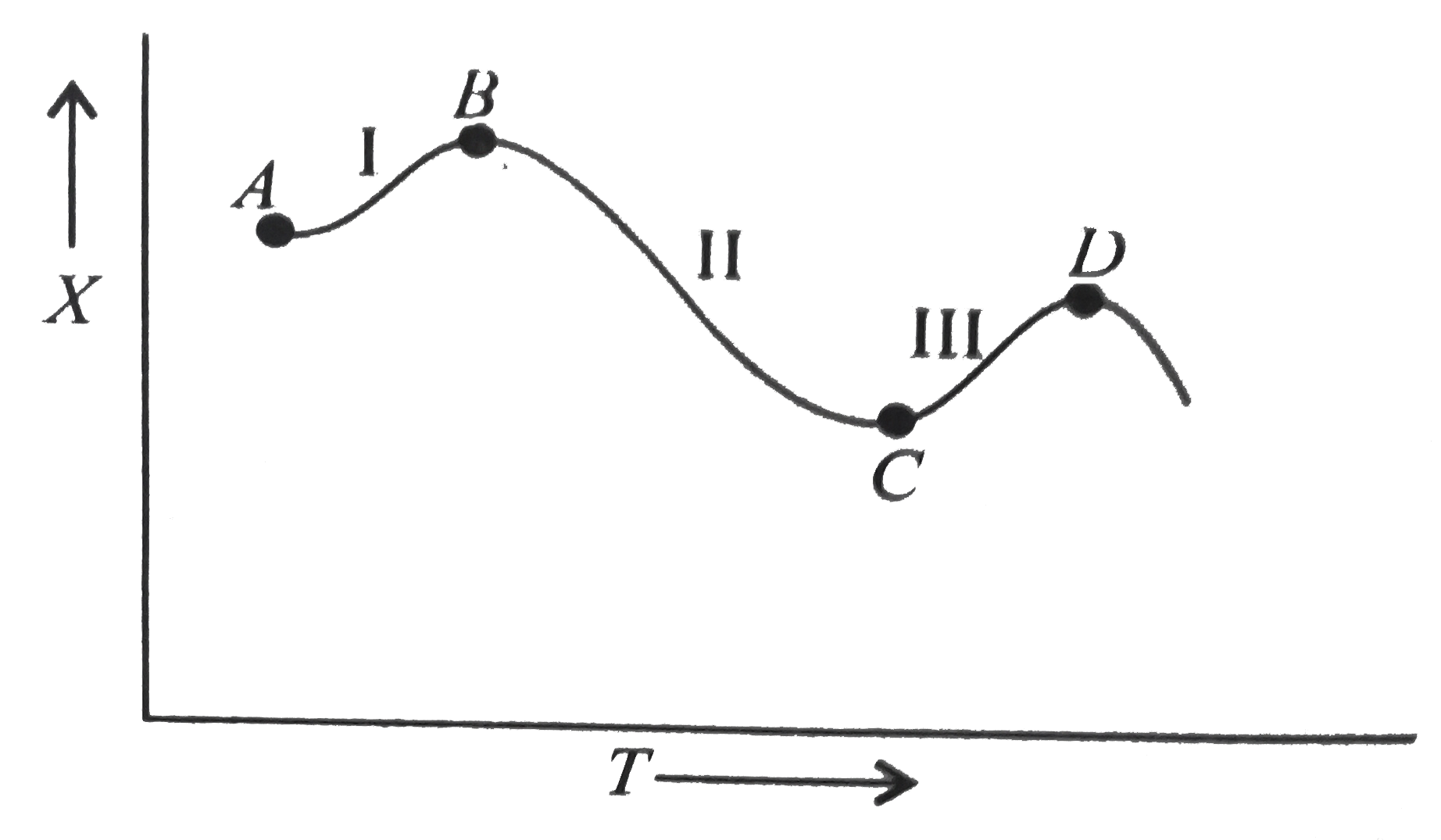
For the following reaction through stages I, II and III
AI−−→BII−−→CIII−−→D
quantity of the product formed (x) varies with temperature (T) as given. Select the correct statement.
View SolutionIf (→a×→b)2+(→a.→b)2=676 and ∣∣∣→b∣∣∣=2 then ∣∣→a∣∣ is equal to
View SolutionIf (→a×→b)2+(→a.→b)2=676 and ∣∣∣→b∣∣∣=2 then ∣∣→a∣∣ is equal to
View SolutionFor the following reaction through stages I, II and III
AI−−→BII−−→CIII−−→D
quantity of the product formed (x) varies with temperature (T) as given. Select the correct statement.

View SolutionIf →a,→b,→c are non-coplanar unit vectors such that
→a×(→b×→c)=(→b+→c)√2, then the angle between →a and →b is
View Solution
