Let a* b =1cm (a,b) for all values of a,b ∈ N
(i) Find (12*16)
(ii) Show that * is commutative on N
(iii) Find the identity element in N
(iv) Find all invertible elements in N
The correct Answer is:(i)48 (iii)1 (iv) 1
(i) 12⋅16=1cm(12,16)=(4×3×4)=48
(ii)a*b=1cm (a,b) =1cm (b,a)=b*a
(iii) let e be the identity element in N
(iv) Let a in N be an arbitrary element
Then a⋅b=1→1cm(a,b)=1→a=b=1
∴ 1 is the only element in N which is ivertible
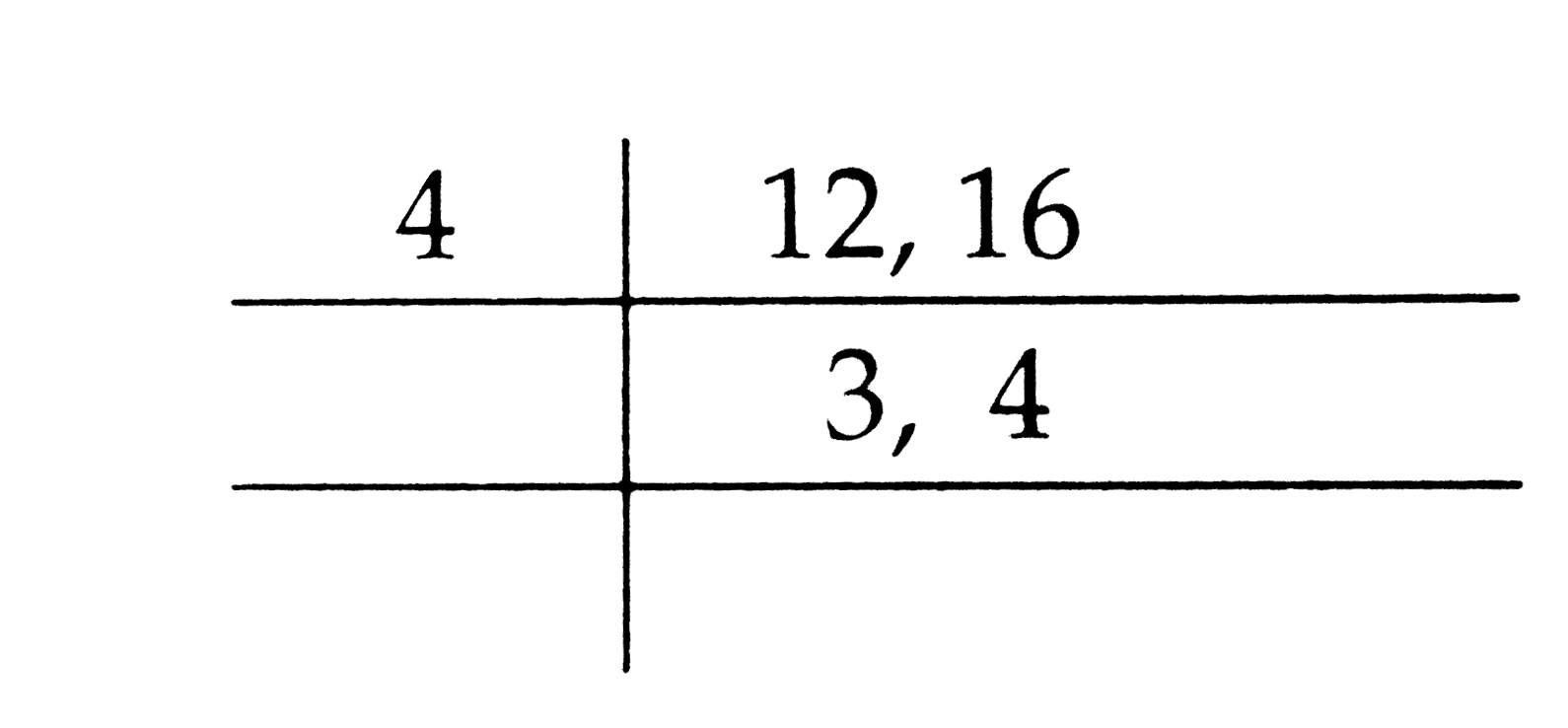
Topper's Solved these Questions
- BINARY OPERATIONSBOOK - RS AGGARWALCHAPTER - BINARY OPERATIONSEXERCISE - Exercise 3B
8 Videos
- BINARY OPERATIONSBOOK - RS AGGARWALCHAPTER - BINARY OPERATIONSEXERCISE - Exercise 3B
8 Videos
- BAYES'S THEOREM AND ITS APPLICATIONSBOOK - RS AGGARWALCHAPTER - BAYES'S THEOREM AND ITS APPLICATIONSEXERCISE - Exercise 30
18 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - RS AGGARWALCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise 9C
9 Videos
Similar Questions
Let * be a binary operation on the set Q0 of all non-zero rational numbers defined by a*b=ab2 , for all a, b∈Q0 . Show that (i) * is both commutative and associative (ii) Find the identity element in Q0 (iii) Find the invertible elements of Q0 .
View SolutionLet Q0 be the set of all nonzero reational numbers Let * be a binary operation on Q0 defined by a*b =ab4 for all a,b ∈Q0
(i) Show that * is commutative and associative
(ii) Find the identity element in Q0
(iii) Find the inverse of an element a in Q0
View SolutionLet 'o' be a binary operation on the set Q0 of all non-zero rational numbers defined by a o b=ab2 , for all a, b∈Q0 . Show that 'o' is both commutative and associate (ii) Find the identity element in Q0 (iii) Find the invertible elements of Q0 .
View SolutionLet '⋅' be a binary operation on N given by a⋅b=L.C.M.a,b for all a,b∈N. Find 5⋅7,20⋅16 (ii) Is * commutative? Is * associative? Find the identity element in N Which element of N are invertible? Find them.
View SolutionLet '⋅' be a binary operation on N given by a⋅b=L.C.M.a,b for all a,b∈N. Find 5⋅7,20⋅16 (ii) Is * commutative? Is * associative? Find the identity element in N Which element of N are invertible? Find them.
View SolutionLet * be a binary operation on Z defined by a*b=a+b−4 for all a, b∈Z. (i)Find the identity element in Z. (ii) Find the invertible elements in Z.
View SolutionLet * be a binary operation on Z defined by a⋅b=a+b−4 for all a, b∈Z. Find the identity element in Z. (ii) Find the invertible elements in Z.
View SolutionShow that the operation * on Z define by
a* b =a+b+1 for all a,b in Z
Satisfies (i) the closure property (ii) the associative law and (iii) the commutative law ltrbgt (iv) find the identity element in Z
(v) what is the inverse iof an element a in Z ?
View SolutionLet ∗be the binary operation on N given by a∗b=LCMof a and b. Find (i) 5∗7,20∗16(ii) Is ⋅commutative? (iii) Is ∗associative? (iv) Find the identity of ∗in N (v) Which elements of N are invert
View SolutionLet ∗be the binary operation on N given by a∗b=LCMof a and b. Find
(i) 5∗7,20∗16
(ii) Is ⋅commutative?
(iii) Is ∗associative?
(iv) Find the identity of ∗in N
(v) Which elements of N are invert
View Solution
