The cable of a uniformly loaded suspension bridge hangs in the form of a parabola. The roadway which is horizontal and 100 m long is supported by vertical wires attached to the cable, the longest wire being 30 m and the shortest being 6 m. Find t
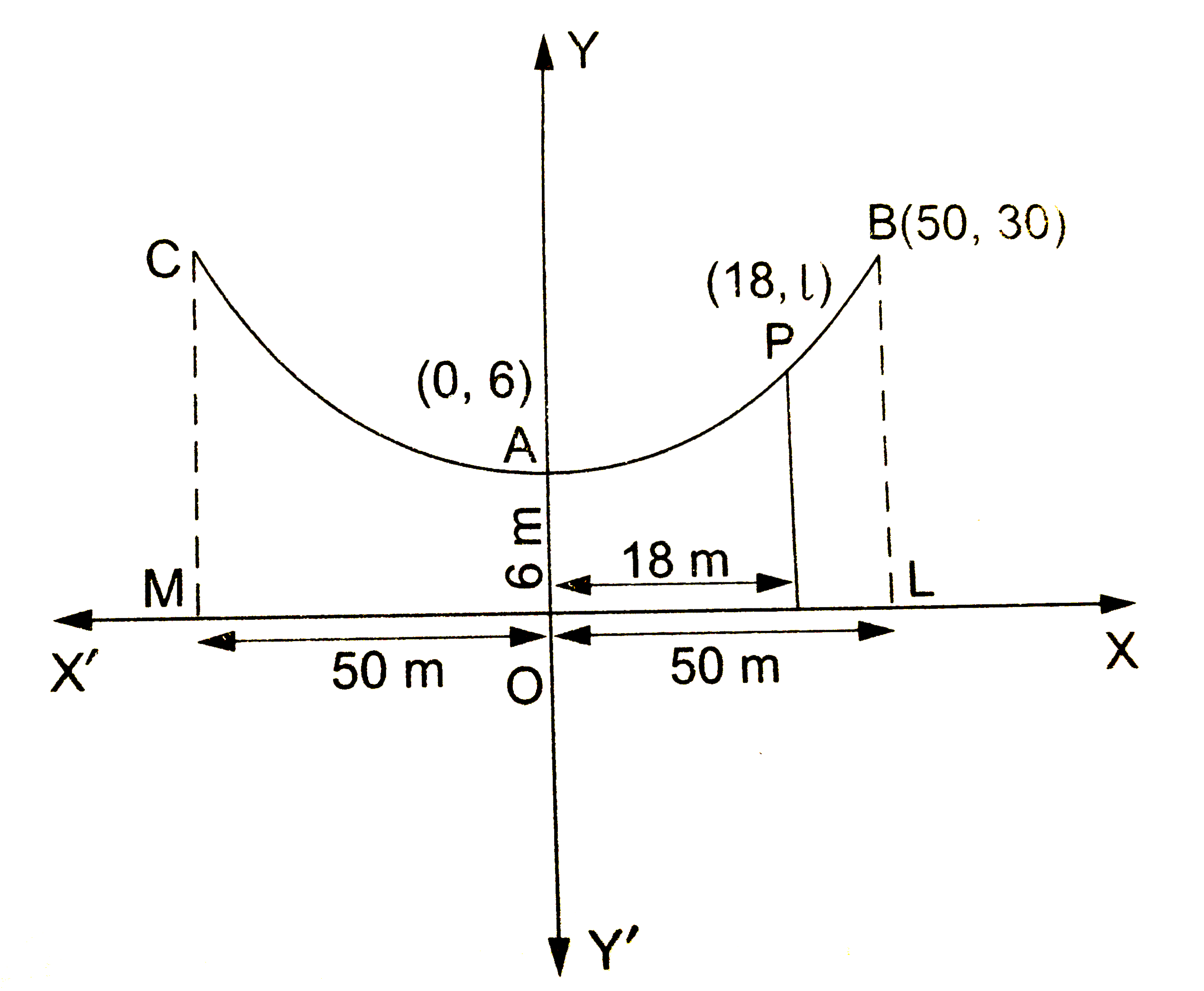
Let X'OX be the x-axis, taken along the roaway, and let YOY' be the y-axis.
Let CAB be the bridge in the form of a parabola having its vertex at A(0, 6) such that A is the centre of the bridge.
Let BL and CM be the longest vertical wires, each of length 30 m, and let OA be the shortest vertical wire, 6 m in length.
The equation of the parabolic form of the bridge is
x2=4a(y−6). ....(i)
It passes through B(50, 30).
Putting x = 50 and y = 30 in (i), we get
2500=4a(30−6)⇒a=250096.
Putting a=250096(y−6)⇒6x2=625y−3750. (ii)
Let l m be the length of the supporting wire 18 m from the middle.
Then, P(18, l) must satisfy (ii).
∴6×18×18=625l−3750⇒625l=5694
⇒l=9.11.
Hence, the length of the supporting wire 18 m from the middle is 9.11 m.
Topper's Solved these Questions
Similar Questions
The cable of a uniformly loaded suspension bridge hangs in the form of a parabola. The roadway which is horizontal and 100m long is supported by vertical wires attached to the cable, the longest wire being 30m and the shortest being 6m. Find the length of the supporting wire attached to the roadway 18m from the middle.
View SolutionIF the distribution of weight is uniform, then the rope of the suspended bridge takes the form of parabola.The height of the supporting towers is 20m, the distance between these towers is 150m and the height of the lowest point of the rope from the road is 3m. Find the equation of the parabolic shape of the rope considering the floor of the parabolic shape of the rope considering the floor of the bridge as X-axis and the axis of the parabola as Y-axis. Find the height of that tower which supports the rope and is at a distance of 30 m from the centre of the road.
View Solution
Knowledge Check
A wire of length l, mass m and resistance R slides without any friction down the parallel conducting rails of negligible resistance . The rails are connected to each other at the bottom by a resistanceless rail parallel to the wire so that the wire and the rails form a closed rectangualr conducting loop. The plane of the rails makes an angle θ with the horizontal and a uniform vertical magnetic field of the inducetion B exists throughout the rregion. Find the steady state velocity of the wire.
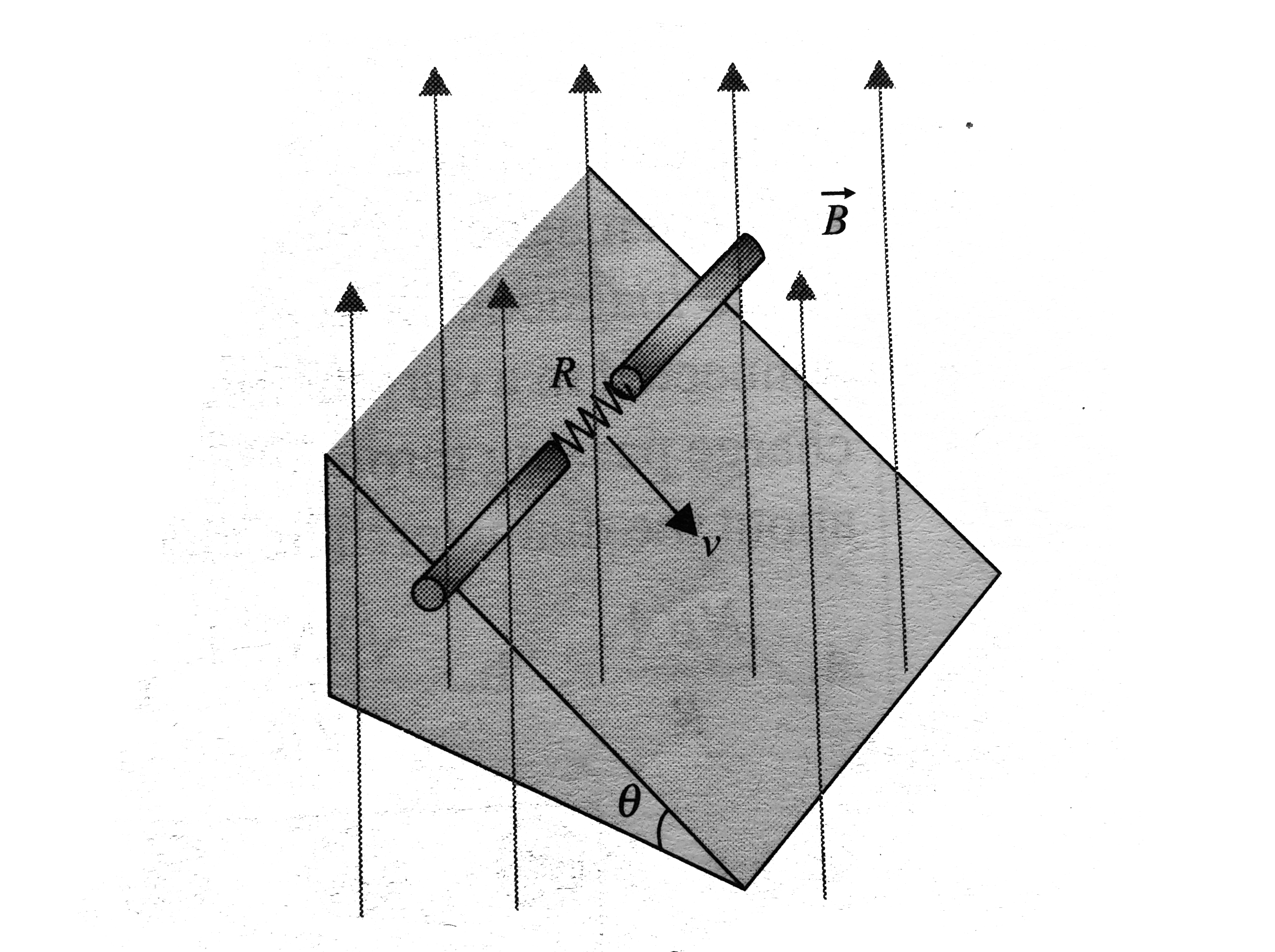 A(a) mgRsinθB2l2cos2θB(b) mgRsin2θB2l2cos2θC( c) mgRsinθB2l2cos2θD( d) mgRsin2θB2l2cosθ
A(a) mgRsinθB2l2cos2θB(b) mgRsin2θB2l2cos2θC( c) mgRsinθB2l2cos2θD( d) mgRsin2θB2l2cosθA brilliant student of physics developed a magnetic balance to weight objects. The mass m to be measured is hung from the center the bar. Bar is kept in a uniform magnetic field of 1.5T directed into the plane of the figure. Battery voltage can be adjusted to vary the current in the circuit. The horizontal bar shown is 60cm long and is made of extremly light weight material. It is connected to the battery via a resistance. There is no tension in the supporting wired. The magnetic force only supports the hanging weight.
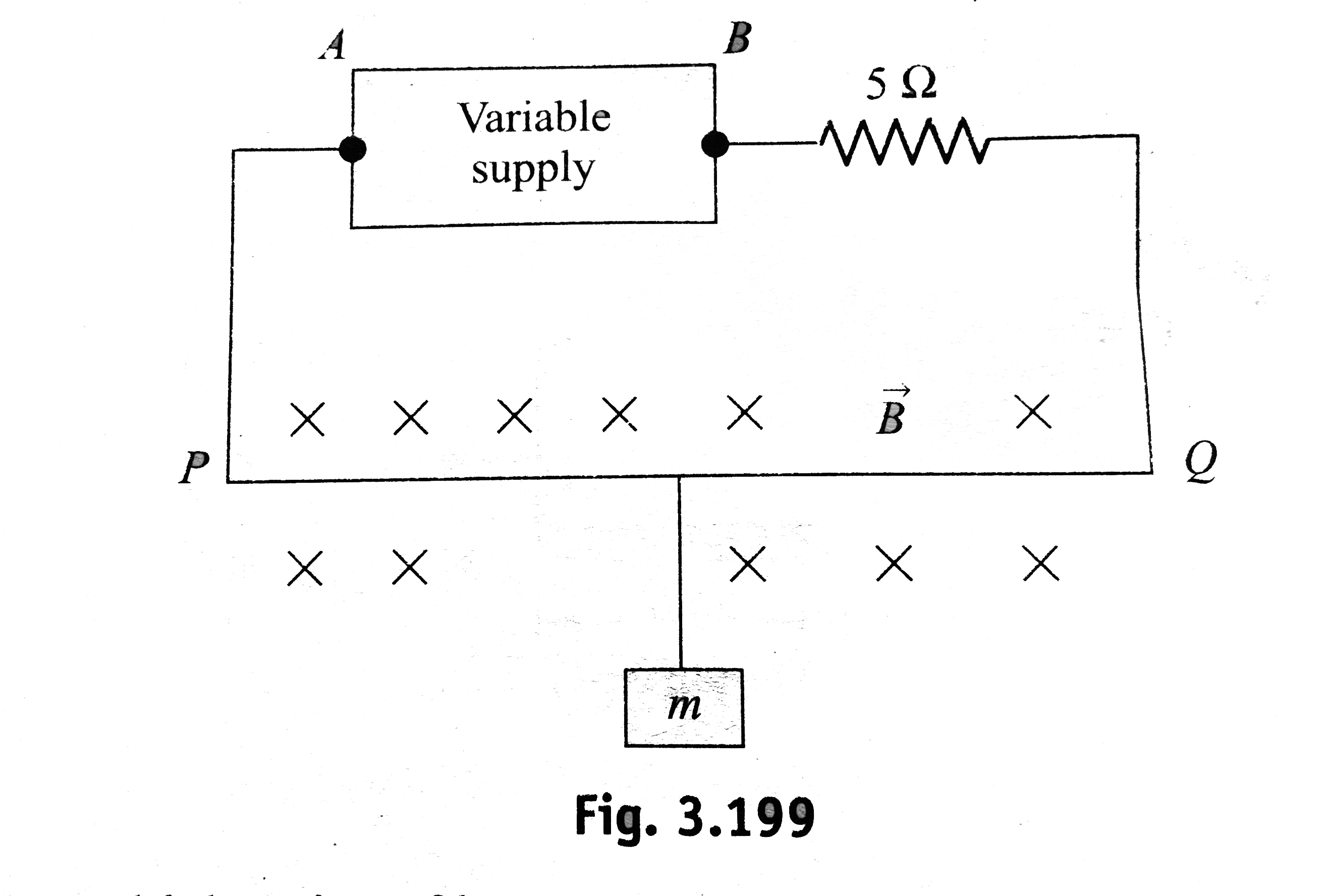
If V=150V, what is the maximum mass m ?A(a) 1.3kgB(b) 1.8kgC(c ) 2.2kgD(d) 2.7kgA brilliant student of physics developed a magnetic balance to weight objects. The mass m to be measured is hung from the center the bar. Bar is kept in a uniform magnetic field of 1.5T directed into the plane of the figure. Battery voltage can be adjusted to vary the current in the circuit. The horizontal bar shown is 60cm long and is made of extremly light weight material. It is connected to the battery via a resistance. There is no tension in the supporting wired. The magnetic force only supports the hanging weight.
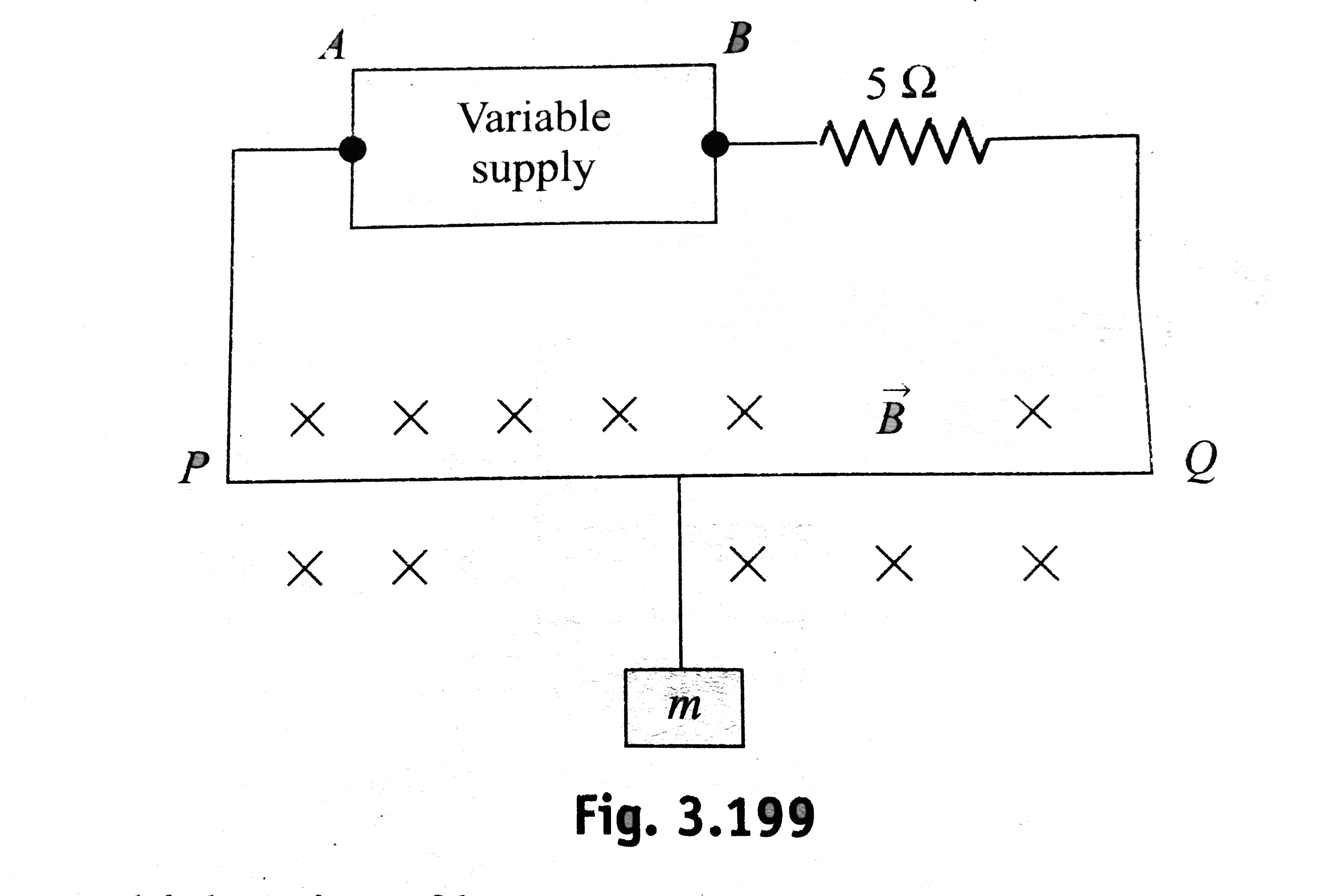
Which point of battery is positive?A(a) AB(b) BC(c ) either AorBD(d) cannot be found because time of rotation is not given.
A wooden disc of mass M and radius R has a single loop of wire wound on its circumference. It is mounted on a massless rod of length d. The ends of the rod are supported at its ends so that the rod is horizontal and disc is vertical. A uniform magnetic field B0 exists in vertically upward direction. When a current I is given to the wire one end of the rod leaves the support. Find least value of I.

View SolutionOne end of a steel wire is attached to a fixed support and the other end is attached to a string, which is going over a pulley and is connected to a block, whch is hanging vertically. It is observed that the wire vibrates in its fundamental mode with frequency of 200 Hz. When the block is submerged in water, the same wire vibrates in its 1 harmonic with frequency of 100 Hz. Density of steel wire is 8000kg/m3 and length of wire is 1 m.

View SolutionA small ball of mass 100g is attached to a light and inextensible string of length 50cm. The string is tied to a support O and the mass m released from point A which is a' a horizontal distance of 30cm from the support. Calculate the speed of the ball is its lowest point of the trajectory.
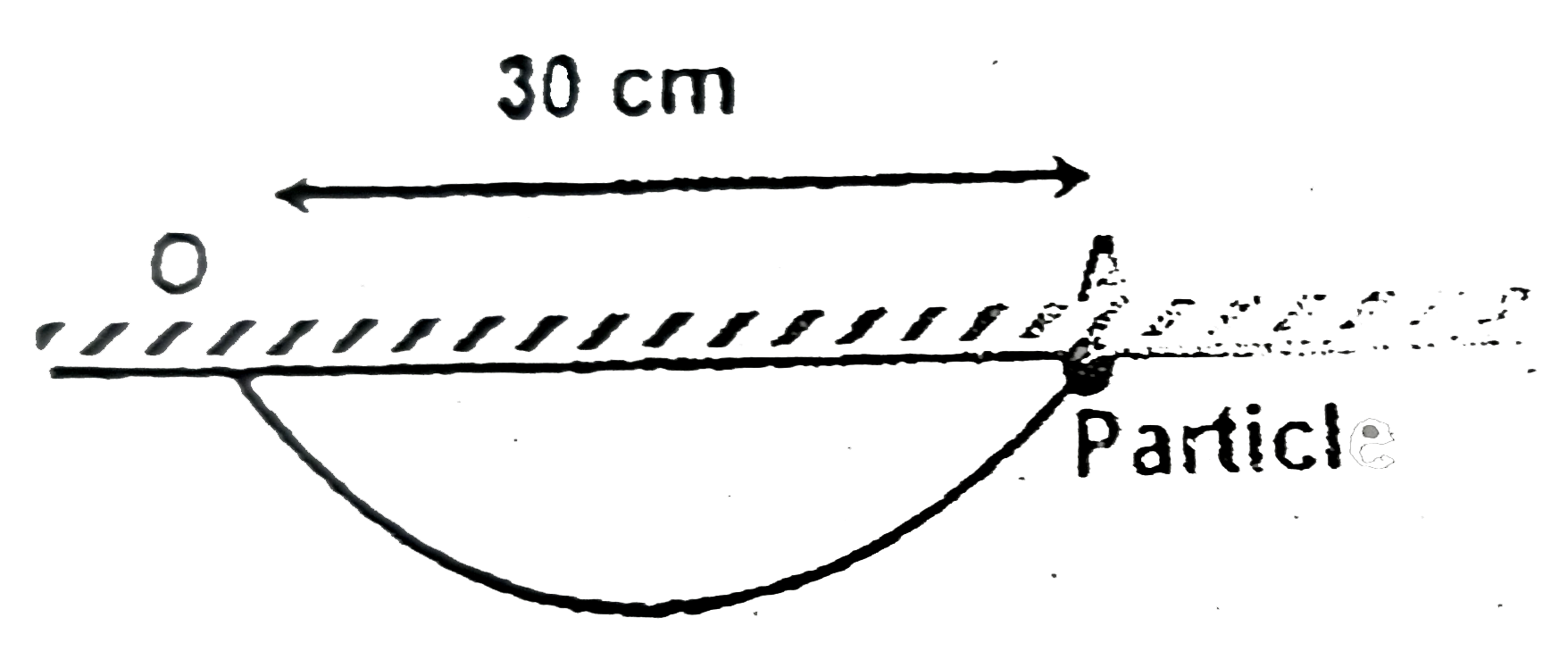
View SolutionA particle B of mass 5 kg is attached to a frictionless pivot A by a thread of length d = 0.2 m so that B hangs freely. At some instant of time a strong wind begins to apply a constant horizontal force F = 100 N to B, as a result it rotates about A in a vertical plane. Find the speed (in m/s) of B at the instant when the string is horizontal (g=10ms2)
View SolutionA current of 10A flows around a closed path in a circuit which is int eh horizontal plne as shown in the figure. The circuit consists oif eight alternating arcs of radii r1=0.08m and r2=0.12m. Each subtends the same angle at the centre.
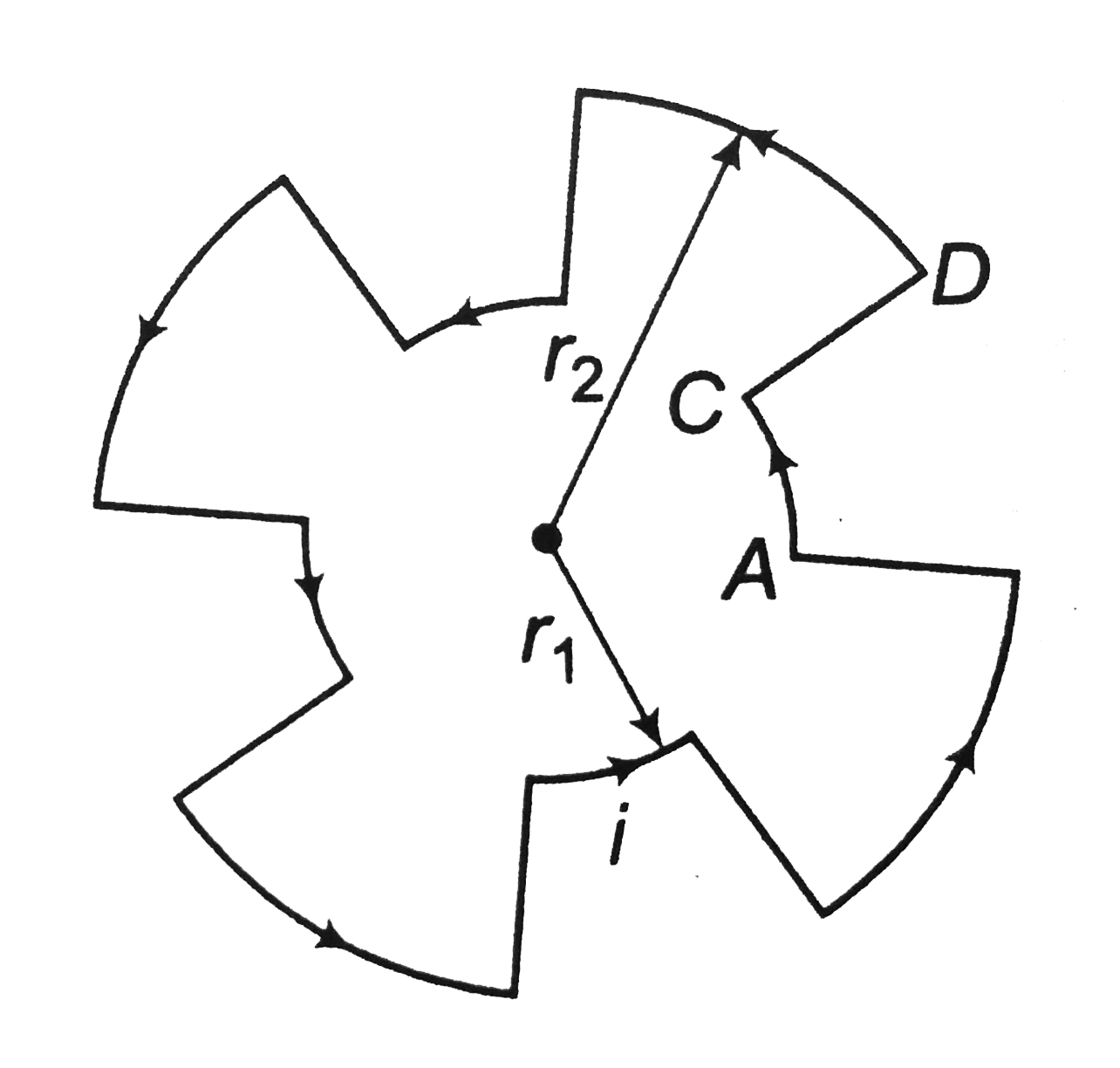
a. Find the magnetic field produced by this circuit at the centre.
b. An infinitely long straight wire carryin as current of 10A is passing through the centre of the above circuit vertically with the direction of the current being into the pane of the circuit. what is the force acting on the wire at the centredue to the curren in the circuit? What is the force acting on the arc AC and the straight segment CD due to the current at the centre?
View Solution
