In the given figure, ABC is a right angled triangle, right -angled at A in which and I is the incentre of .
Find the area of the shaded region. [Take ]
![In the given figure, ABC is a right angled triangle, right -angled at A in which AB=6 cm, BC=10 cm and I is the incentre of DeltaABC. Find the area of the shaded region. [Take pi=3.14]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/RSA_MATH_X_C16_S01_033_Q01.png)
From right , we have
Let the radius of the incricle be . Then

area of the shaded region ltbgt
Hence the required area is
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - AREA OF CIRCLE, SECTOR AND SEGMENT EXERCISE - SOLVED EXAMPLE_TYPE1videos
AREA OF CIRCLE, SECTOR AND SEGMENT
- BOOK - RS AGGARWALCHAPTER - AREA OF CIRCLE, SECTOR AND SEGMENT EXERCISE - Exercise 16A65videos
AREA OF CIRCLE, SECTOR AND SEGMENT
- BOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)30videos
ARITHMETIC PROGRESSION
Similar Questions
In the given figure, ABC is a right angled triangle, right -angled at A in which AB=6cm,BC=10cm and I is the incentre of ΔABC.
Find the area of the shaded region. [Take π=3.14]
 View Solution
View SolutionIn the given figure PQ=24cm,PR=78cm and O is the centre of the circle. Find the area of the shaded region. [Take π=3.14]
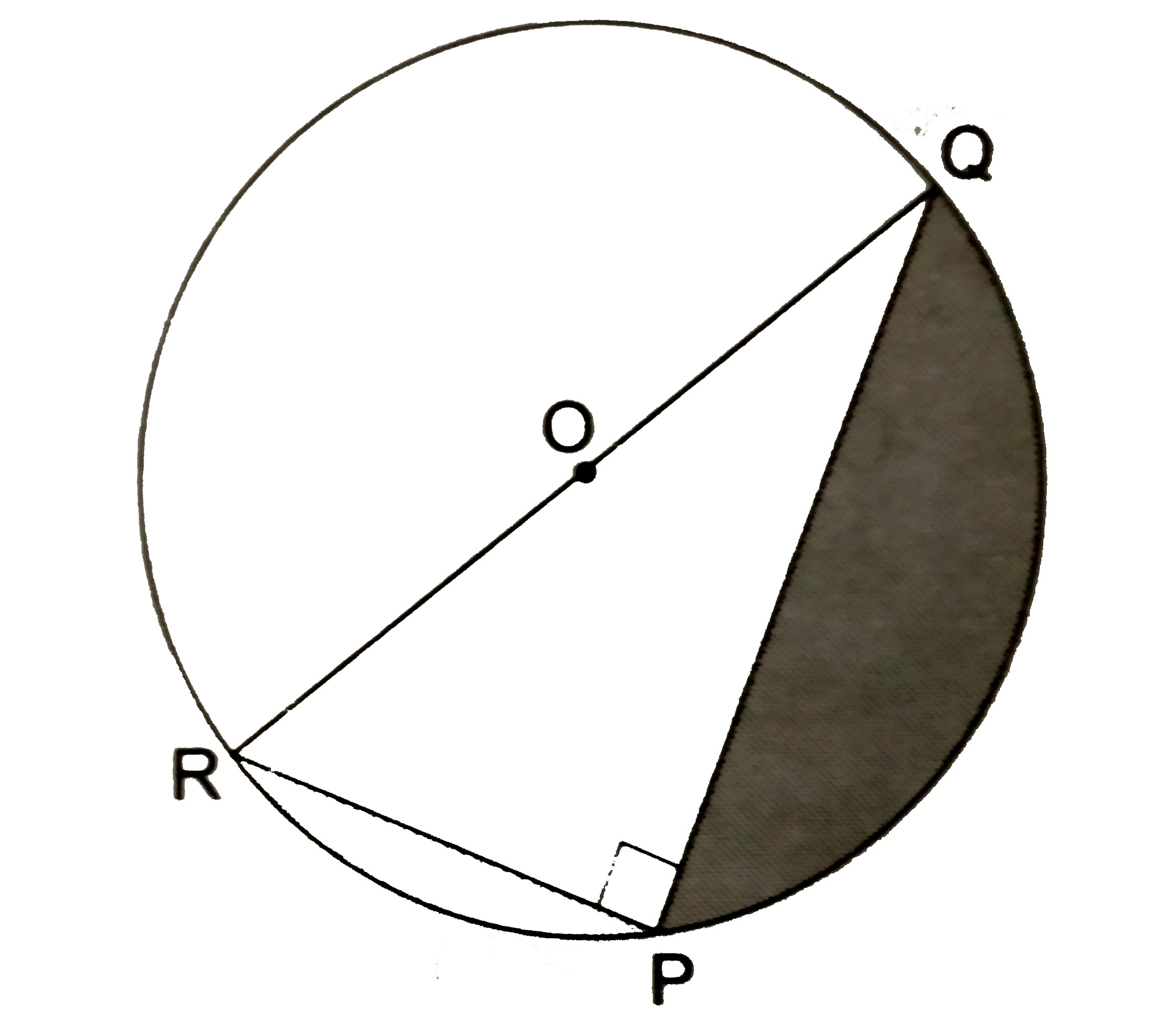 View Solution
View SolutionIn the given figure,ABC in a right-angled triangle,right-angled atB.IfBC=5cmandAC-AB=1cm,f∈dthevalueofcosecAandcos A
View SolutionIn the following figure, ABC is a right angled triangle at A. Find the area of the shaded region If AB = 6 cm, BC = 10 cm and I is the center of incircle of ΔABC
View SolutionIn the given figure,ABC is a right angled triangle in which ∠A=90∘,AB=21 cm and AC=28 cm.Semi-circles are drawn on AB, BC and AC as diameters. Find the area of shaded region.
View SolutionIn the given figure, △ABC is an isosceles triangle right angled at C with AC = 4 cm. Find the length of AB.
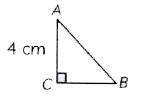 View Solution
View SolutionConstruct a right triangle, right angled at C in which AB=5.2\ cm and BC=4.6 cm.
View SolutionABC is a right triangle, right angled at C and AB=√2BC. Then, find ∠ABC.
View SolutionΔABC is a right angle triangle (right angled at B), BD is perpendicular to AC. If AC=16cmBC=9cm, find the length of CD.
View SolutionIn the given figure, ΔABC is right angled at A. Find the area of the shaded region if AB = 6 cm, BC = 10 cm and O is the centre of the incricle of ΔABC. (Use π=3.14)
 View Solution
View Solution

