In the given figure ΔABC is a right angled triangle with ∠B=90∘,AB=48cm and BC=14cm. With AC as diameter a semicircle is drawn and with BC as radius, a quadrant of a circle is drawn. Find the area of the shaded region.
[Use π=227]
![In the given figure DeltaABC is a right angled triangle with /B=90^(@),AB=48cm and BC=14cm. With AC as diameter a semicircle is drawn and with BC as radius, a quadrant of a circle is drawn. Find the area of the shaded region. [Use pi=22/7]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/RSA_MATH_X_C16_S01_041_Q01.png)
In right ΔABC, we have
AC2=AB2+BC2=(48)2+(14)2=(2304+196)=2500
⇒AC=√2500=540cm⇒R=502cm=25cm
Area of the shaded region
=ar(ΔABC)+(area of semicircle onAC)−ar(quadrantBCD)
=(12×14×48)+12π×25×25−14π×BC2
[336+12×227×625−14×227×14×14]cm2
=(336+68757−154)cm2=(182−982−14)cm2
=1164.14cm2
Hence the area of the shaded region is 1164.14cm2
Topper's Solved these Questions
- AREA OF CIRCLE, SECTOR AND SEGMENT BOOK - RS AGGARWALCHAPTER - AREA OF CIRCLE, SECTOR AND SEGMENT EXERCISE - SOLVED EXAMPLE_TYPE
1 Videos
- AREA OF CIRCLE, SECTOR AND SEGMENT BOOK - RS AGGARWALCHAPTER - AREA OF CIRCLE, SECTOR AND SEGMENT EXERCISE - Exercise 16A
65 Videos
- ARITHMETIC PROGRESSIONBOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)
30 Videos
Similar Questions
In the given figure, ∠B=90∘,AB=28cmandBC=21 cmwith AC as diameter a semi-circle is drawn and with BC asradius a quarter circle is drawn. Find the area of theshaded region.
View SolutionIn Figure, ABC is a right-angled triangle, ∠B=900,AB=28cm and BC=21cm. With AC as diameter a semicircle is drawn and with BC as radius a quarter circle is drawn. Find the area of the shaded region correct to two decimal places.
View Solution
Knowledge Check
In the figure, ABC is a right angled triangle with B = 90∘ , BC = 21 cm and AB = 28 cm. With AC as diameter of a semicircle and with BC as radius, a quarter circle is drawn. Find the area of the shaded portion correct to two decimal places
 A428.75cm2B857.50cm2C214.37cm2D371.56cm2
A428.75cm2B857.50cm2C214.37cm2D371.56cm2
In the figure, in ΔABC,∠B=90∘,AB=28cmandBC=21cm. With AC as diameter a semicircle is drawn and with BC as radius a quarter circle is drawn. Find the area of the shaded region correct to two decimal places.
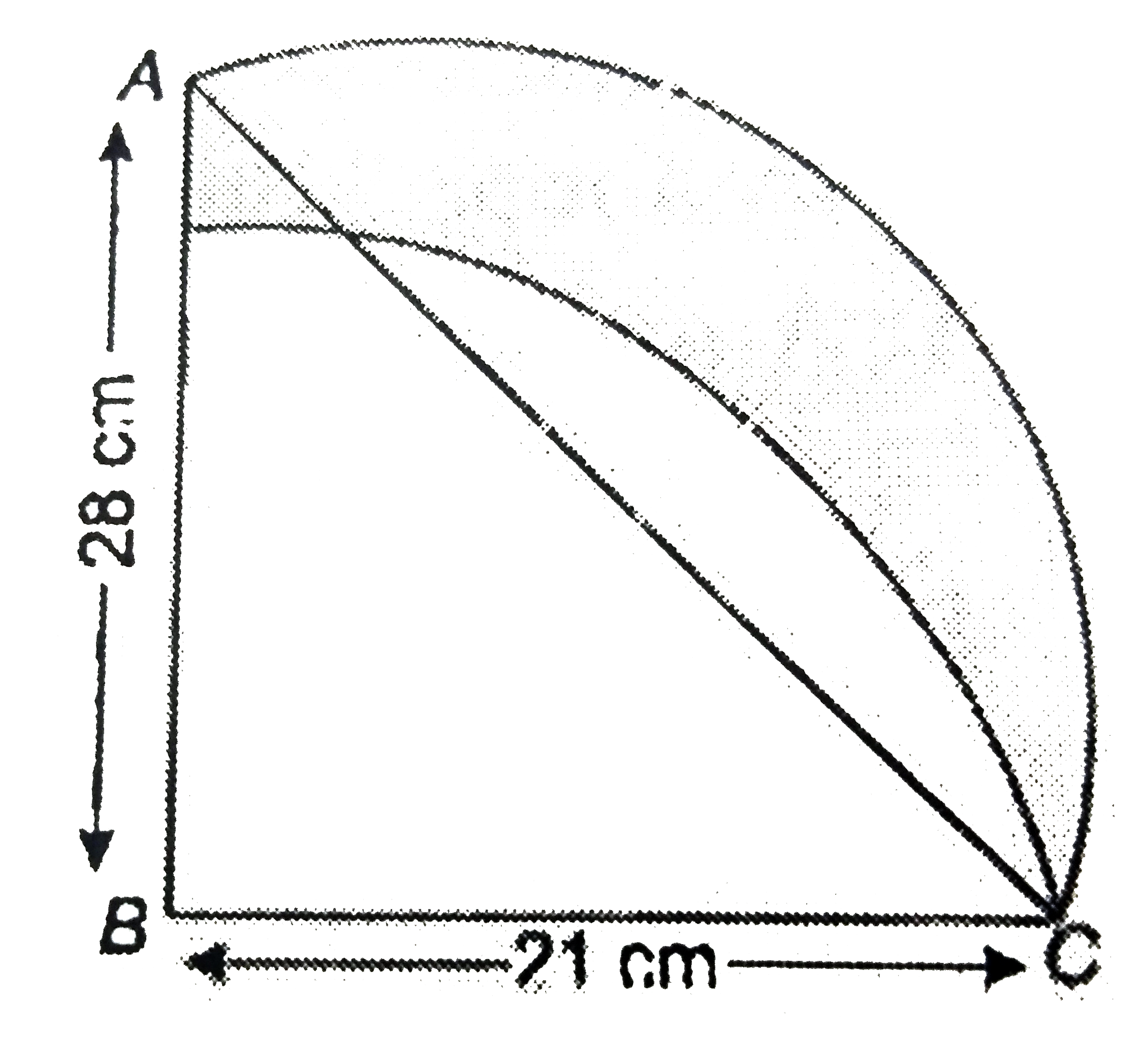
View SolutionABCP is a quadrant of a circle of radius 14 cm. with AC as diameter, a semicircle is drawn. Find the area of the shaded portion
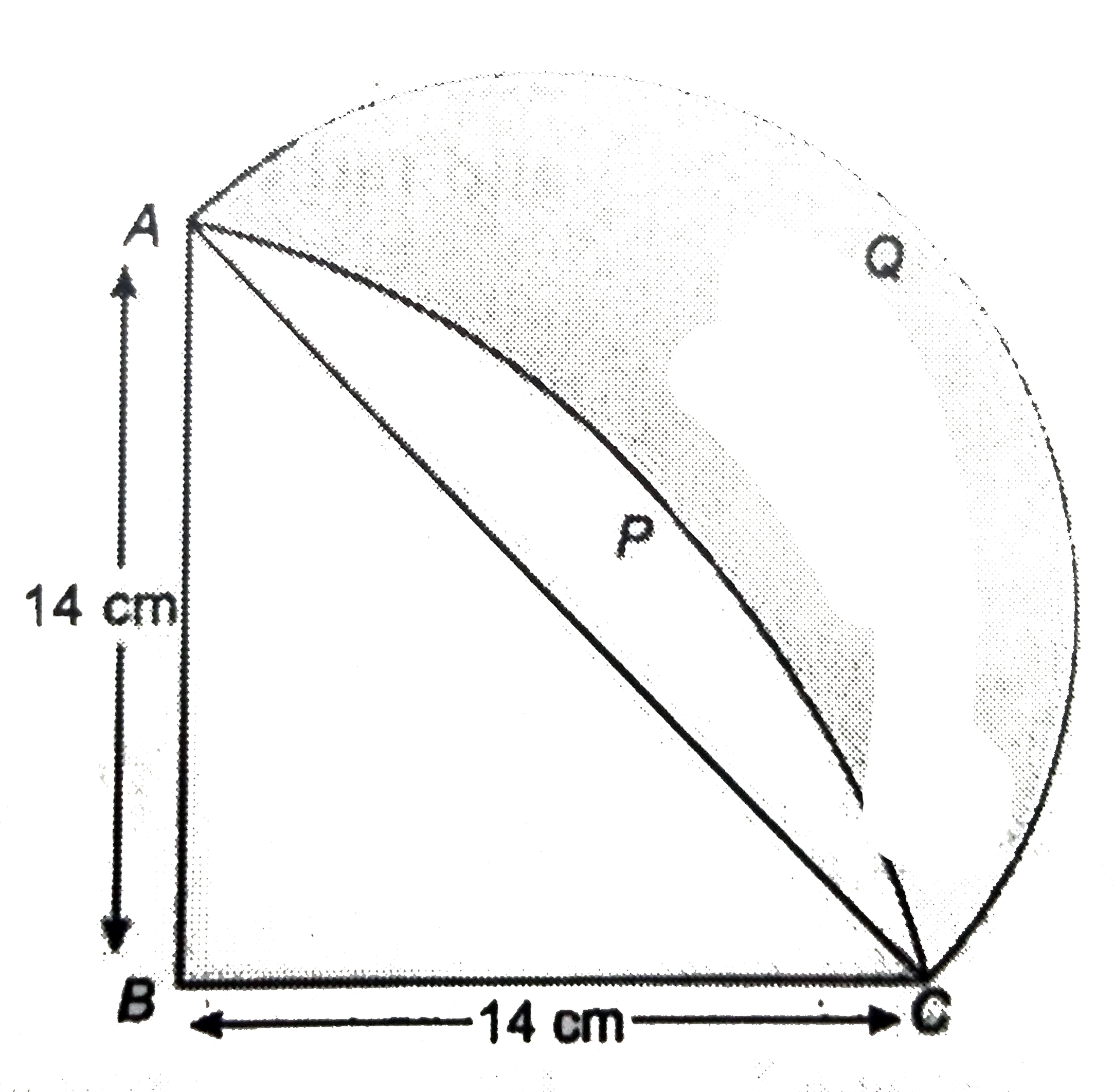
View SolutionBCP is a quadrant of a circle of radius 14cm. With AC as diameter, a semi-circle is drawn. Find the area of the shaded portion.
View SolutionABCP is a quadrant of a circle of radius 14 cm. With AC as diameter, a semi-circle is drawn. Find the area of the shaded portion.
View SolutionIn the adjoining figure, ΔABC is a right-angled triangle in which ∠B=90∘, ∠A=30∘ and AC=20cm. Find (i)BC, (ii)AB.

View SolutionIn the given figure,ABC is a right angled triangle in which ∠A=90∘,AB=21 cm and AC=28 cm.Semi-circles are drawn on AB, BC and AC as diameters. Find the area of shaded region.
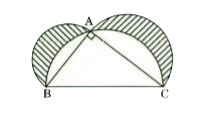
View SolutionIn the figure given below, ABC is a right-angled triangle where ∠A=90∘, AB = p cm and AC = q cm. On the three sides as diameters semicircles are drawn as shown in the figure. The area of the shaded portion, in square cm, is
View Solution
