A chord of a circle of radius 10 cm subtends a right angle at the centre. The area of the minor segments (given π=3.14) is
The correct Answer is:28.5cm2
ar(minor segment)
= ar(sector OACBO)−ar(ΔOAB)
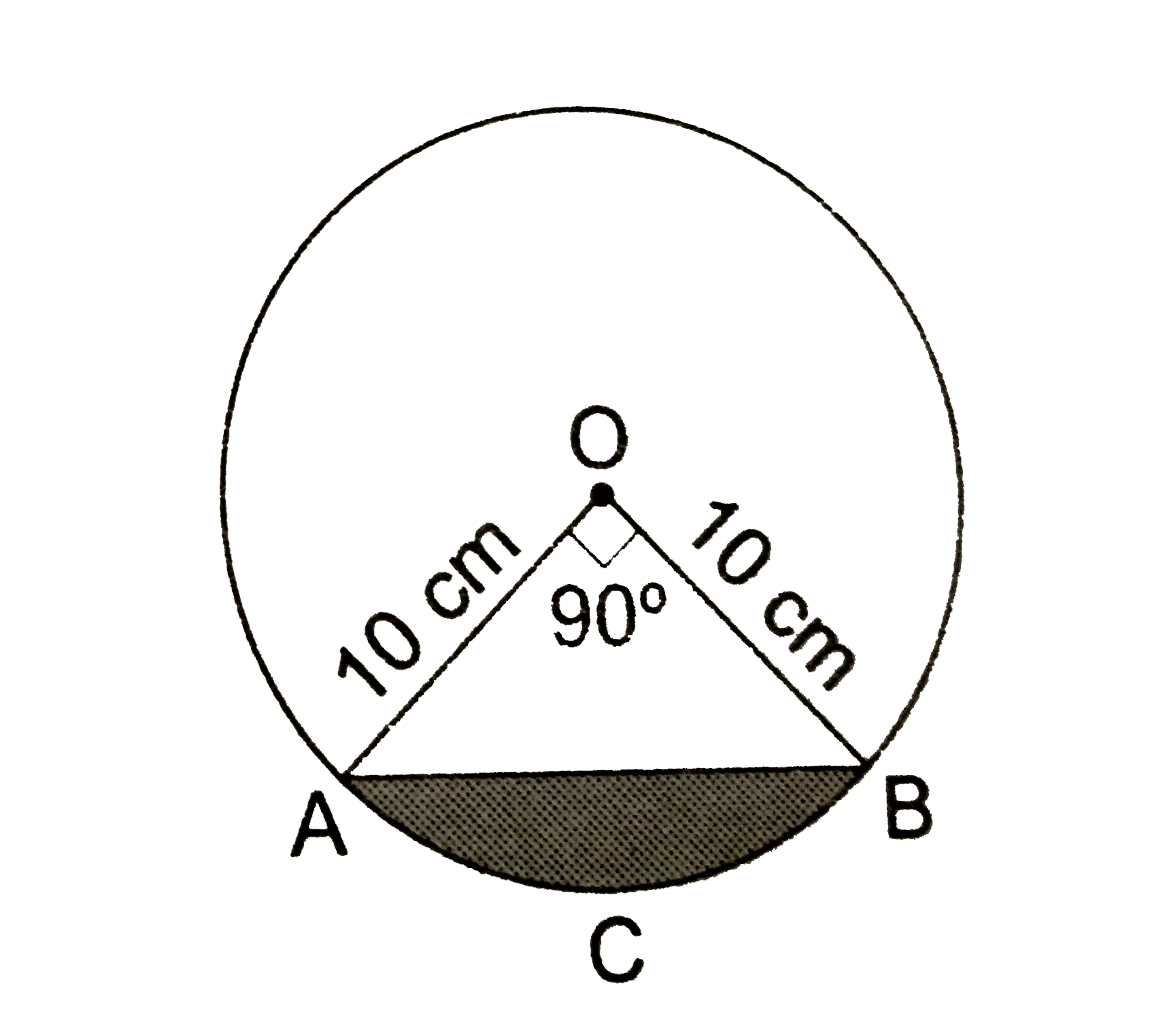
={(3.14×10×10×90360)−(12×10×10)}cm2
=(78.5−50)cm2=28.5cm2
Topper's Solved these Questions
- AREA OF CIRCLE, SECTOR AND SEGMENT BOOK - RS AGGARWALCHAPTER - AREA OF CIRCLE, SECTOR AND SEGMENT EXERCISE - EXERCISE
1 Videos
- AREA OF CIRCLE, SECTOR AND SEGMENT BOOK - RS AGGARWALCHAPTER - AREA OF CIRCLE, SECTOR AND SEGMENT EXERCISE - Exercise 16B
51 Videos
- AREA OF CIRCLE, SECTOR AND SEGMENT BOOK - RS AGGARWALCHAPTER - AREA OF CIRCLE, SECTOR AND SEGMENT EXERCISE - SOLVED EXAMPLE_TYPE
1 Videos
- ARITHMETIC PROGRESSIONBOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)
30 Videos
Similar Questions
Knowledge Check
A chord of circle of a radius 28 cm subtends a right angle at the centre. What is the area of the minor sector?
A621cm2B616cm2C718cm2D721cm2The chord of a circle of radius 10cm subtends a right angle at its centre. The length of the chord (in cm) is
A5√2B5√2C10√2D10√3
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding sector.
View SolutionA chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding :
Minor segment
View SolutionA chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding :
(i) minor segment
(ii) major sector.
View SolutionThe chord of a circle of radius 8 cm subtends a right angle at its centre. Find the length of the chord.
View SolutionA chord AB of a circle of radius 10cm subtends a right angle at the centre. Find: area of the minor sector area of the minor segment area of the major sector area of the major segment
View SolutionA chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding :
Major sector
View Solution
