A point C is called the midpoint of a line segment ¯¯¯¯¯¯AB if
C is an intrerior points of AB
AC =CB
C is an interior point of AB such that ¯¯¯¯¯¯AC=¯¯¯¯¯¯CB
AC+CB=AB
The correct Answer is:C
A point C is called the midpoint of line segment ¯¯¯¯¯¯AB if C is na interiro point of ¯¯¯¯¯¯AB such that ¯¯¯¯¯¯AC=¯¯¯¯¯¯CB
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - INTRODUCTION TO EUCLID'S GEOMETRYEXERCISE - Exercise 62videos
INTRODUCTION TO EUCLID'S GEOMETRY
- BOOK - RS AGGARWALCHAPTER - GEOMETRICAL CONSTRUCTIONSEXERCISE - Exercise 132videos
GEOMETRICAL CONSTRUCTIONS
- BOOK - RS AGGARWALCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Multiple Choice Questions (Mcq)24videos
LINEAR EQUATIONS IN TWO VARIABLES
Similar Questions
In Question 4,
(If a point C lies between two points A and B such that AC = BC, then prove thatAC=12AB.Explain by drawing the figure).
Point C is called a mid-point of line segment AB. Prove that every line segment has one and only one mid-point.View SolutionIn question I, point C is called a mid-point of line segment AB. Prove that every line segment has one and only one mid-point.
 View Solution
View SolutionFind the co-ordinates of point P if P is the midpoint of a line segment AB with A(−4,2)andB(6,2)
View SolutionIn give figur l||m and M is the mid-point of a line segment AB .Show that M is also the mid- point of any line segment CD,having its end points on l and m,respectively.
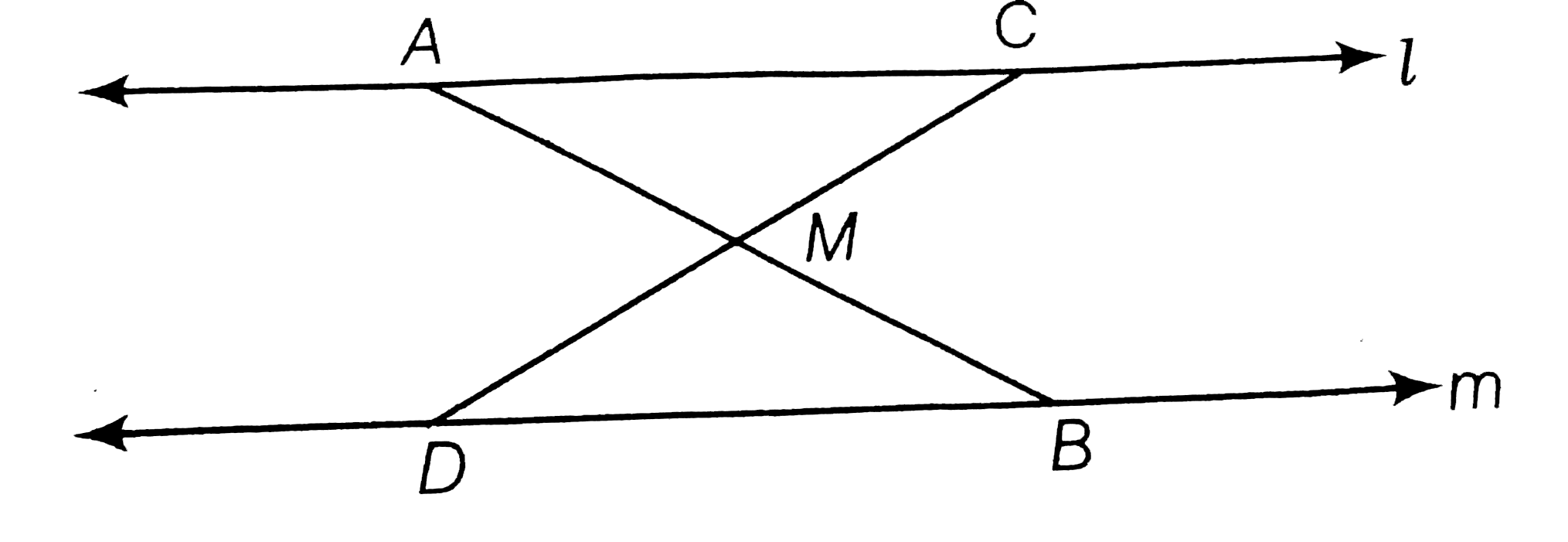 View Solution
View SolutionIn Figure, lm and M is the mid-point of the line segment AB. Prove that M is also the mid-point of any line segment CD having its end-points on l and m respectively.
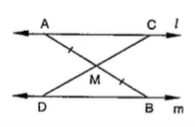 View Solution
View SolutionIn Figure, AP and BQ are perpendiculars to the line segment AB and AP=BQ . Prove that O is the mid-point of line segment AB and PQ
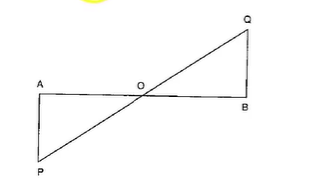 View Solution
View Solution
If A, B are the point on the circle. The line segment ¯¯¯¯¯¯AB is called _______ of the circle.View SolutionThe position vectors of the points A,B with respect to O are ¯a and ¯b and c is mid point of line segment ¯¯¯¯¯¯AB then ¯¯¯¯¯¯OC=
View SolutionIn figure l||m and M is the mid-point of the line segment AB. Prove that M is also the mid-point of line segment CD.
 View Solution
View SolutionFind the value of a, for which point P(a3,2) is the midpoint of the line segment joining the points Q(−5,4)andR(−1,0).
View Solution

