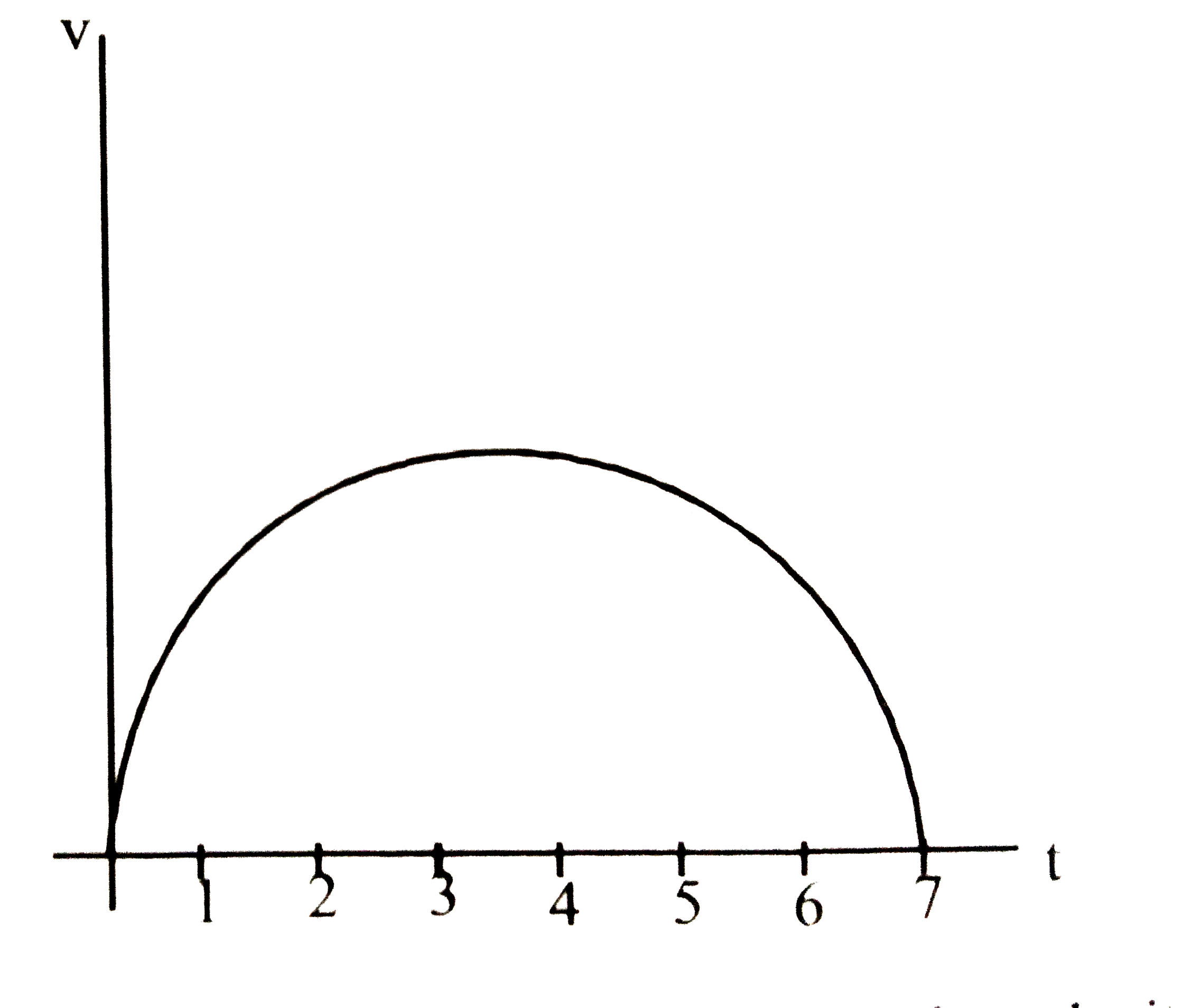
The plot given above represents the velocity of a particle (in mis) with time (in seconds). Assuming that the plot represents a semi-circle, distance traversed by the particle at the end of 7 seconds is approximately.
A
19 m
B
7 m
C
3.2 m
D
4.75 m
Video Solution
Text Solution
The correct Answer is:A
Area of the velocity-time plot (graph): represents the displacement of that object.
Radius of the semi=circle
Area of the semi-circle
=displacement of the particle
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The figure shows the velocity (v) of a particle plotted against time (t).
 AThe particle changes its direction of motion at some point.BThe acceleration of the particle remains constantCThe displacement of the particle is zeroDThe initial and final speeds of the particle are the same
AThe particle changes its direction of motion at some point.BThe acceleration of the particle remains constantCThe displacement of the particle is zeroDThe initial and final speeds of the particle are the sameThe variation of velocity of a particle with time moving along a straight line is illustrated in the following figure. The distance travelled by the particle in four seconds is.
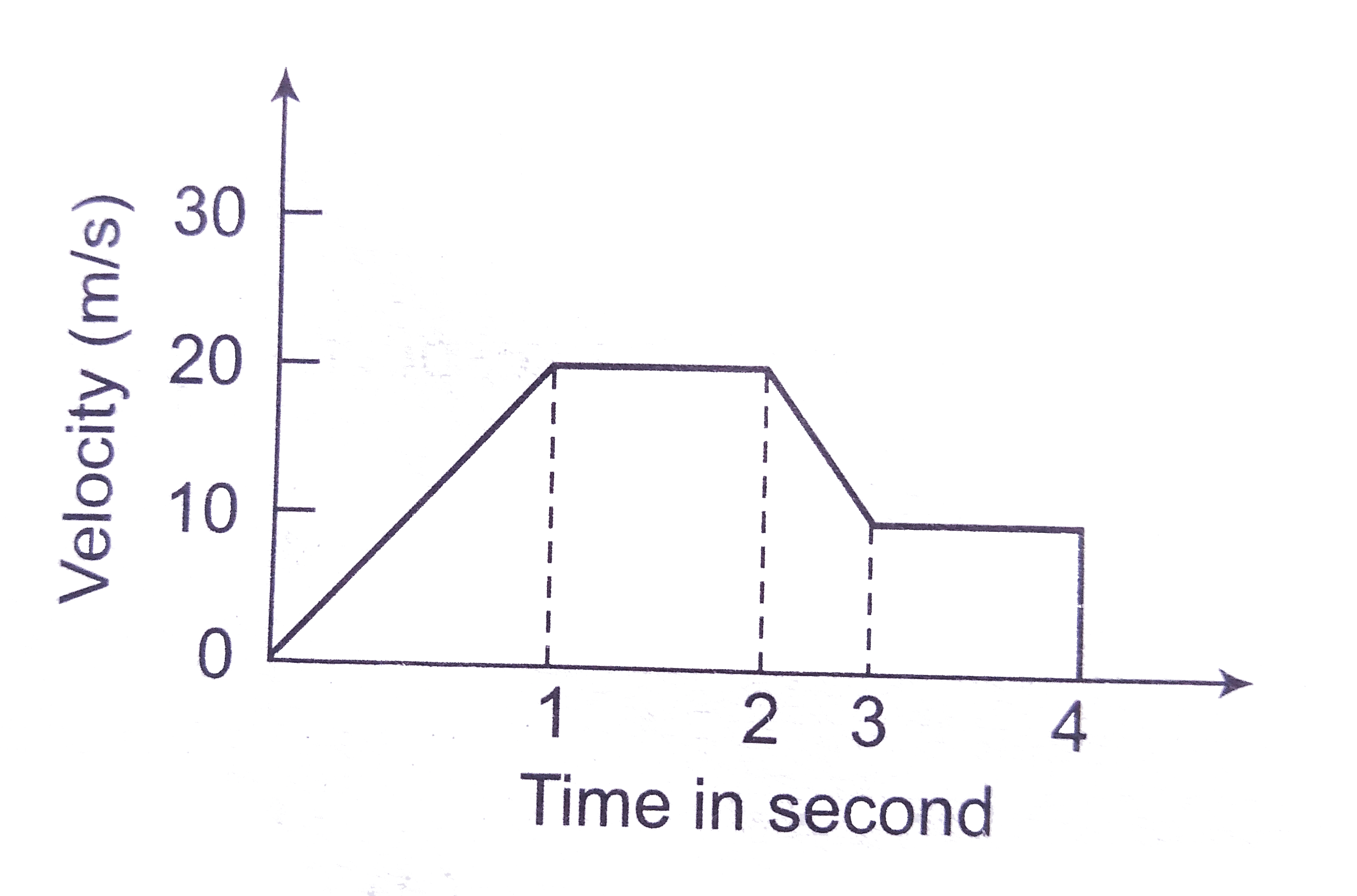 A60 mB55 mC25 mD30 m
A60 mB55 mC25 mD30 mThe velocity time plot for a particle moving on straight line is shown in the figure.
 AThe particle has a constant accelerationBThe particle has nevedr turned aroundCThe paeticle has zero displacement.DThe average speed in the interval 0 to 10 s is the same as the average speed in the interval 10 s to 20s.
AThe particle has a constant accelerationBThe particle has nevedr turned aroundCThe paeticle has zero displacement.DThe average speed in the interval 0 to 10 s is the same as the average speed in the interval 10 s to 20s.
The variation of velocity of particle moving along a straight line is shown in the figure. The distance travelled by the particle in 4th second is?
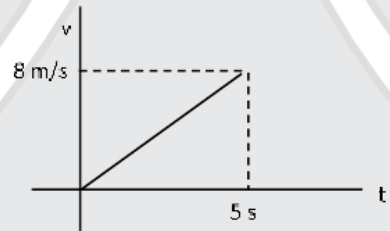
View SolutionSpeed time graph of a particle shown in figure. Find distance travelled by particle in 5second.
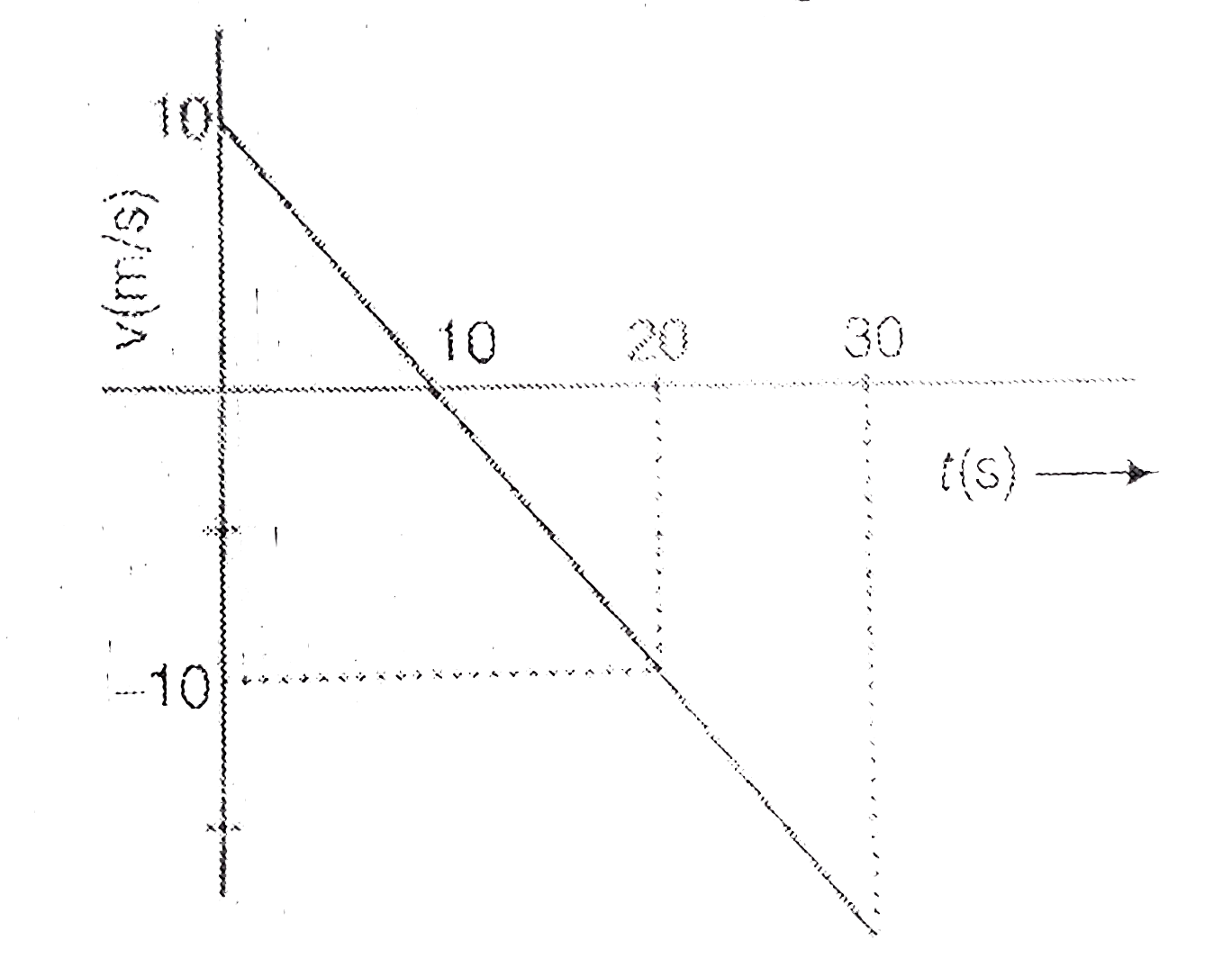
View SolutionThe velocity-time plot for a particle moving on a straight line is shown in the figure, then
View SolutionAssertion : Distance travelled by the particle in the nth second has dimensios of length.
Reason :It is the distance travelled by the partical in the given time.
View SolutionIf the displacement x of a particle (in metre) is related with time (in second) according to relation
x=2t3−3t2+2t+2
find the position, velocity and acceleration of a particle at the end of 2 seconds.
View Solution
