If the potential difference applied to an X-ray tube is doubed while keeping the separation between the filament and the target as same, what will happen to the cutoff wavelength?
Will remain same
Will be doubled
Will be halved
Will be four times of the original wavelength
The correct Answer is:c
To solve the problem regarding the effect of doubling the potential difference on the cutoff wavelength in an X-ray tube, we can follow these steps:
1. Understanding the relationship between potential difference and energy:
The energy (E) of the electrons accelerated in the X-ray tube is given by the equation:
E=eV
where e is the charge of the electron and V is the potential difference.
2. Relating energy to wavelength:
The energy of a photon is also related to its wavelength (λ) by the equation:
E=hcλ
where h is Planck's constant and c is the speed of light.
3. Setting up the cutoff wavelength:
The cutoff wavelength (λ_min) can be derived from the energy equation:
eV=hcλmin
Rearranging this gives:
λmin=hceV
4. Effect of doubling the potential difference:
If the potential difference V is doubled (i.e., V′=2V), we can substitute this into the equation for the cutoff wavelength:
λ′min=hce(2V)=hc2eV=12⋅hceV=12λmin
5. Conclusion:
Therefore, when the potential difference is doubled, the cutoff wavelength is halved:
λ′min=12λmin
Final Answer:
The cutoff wavelength will be halved when the potential difference applied to the X-ray tube is doubled.
The energy (E) of the electrons accelerated in the X-ray tube is given by the equation:
E=eV
where e is the charge of the electron and V is the potential difference.
The energy of a photon is also related to its wavelength (λ) by the equation:
E=hcλ
where h is Planck's constant and c is the speed of light.
The cutoff wavelength (λ_min) can be derived from the energy equation:
eV=hcλmin
Rearranging this gives:
λmin=hceV
If the potential difference V is doubled (i.e., V′=2V), we can substitute this into the equation for the cutoff wavelength:
λ′min=hce(2V)=hc2eV=12⋅hceV=12λmin
Therefore, when the potential difference is doubled, the cutoff wavelength is halved:
λ′min=12λmin
The cutoff wavelength will be halved when the potential difference applied to the X-ray tube is doubled.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
If the potential difference V applied to the coolidge tube is doubled, then the cut off wavelength
AIs doubledBIs halvedCRemains unchangedDIs quadrupled - Question 2 - Select One or More
The potential difference applied to an X-ray tube is increased. As a result, in the emitted radiation,
Athe intensity increasesBthe minimum wavelength increasesCthe intensity remains unchangedDthe minimum wavelength decreases - Question 3 - Select One or More
The potential different applied to an X-rays tube is increase .As a result , in the emitted radiation
Athe intersity increaseBthe minimum wavelength increasresCthe intencity remain unchangedDthe minimum wavelength decrease
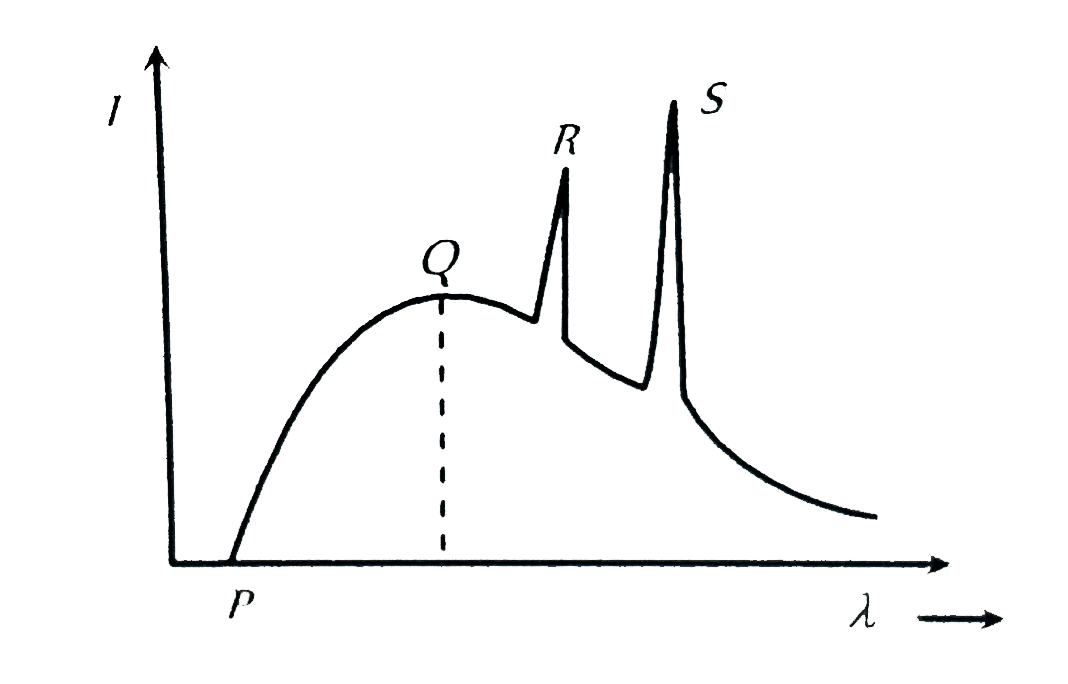
If the potential difference applied across x-ray tube is V volts, then approximately minimum wavelength of the emitted X-rays will be
View SolutionA potential difference of 30 kV is applied across an X-ray tube. Find the minimum wavelength of X-ray generated .
View SolutionA potential difference of 30KV is applied across an X-ray tube. Find the minimum wavelength of X-ray generated.
View SolutionThe potential difference applied to an X-ray tube is 5 kV and the current through it is 3.2 mA. Then the number of electros striking the target par second is
View SolutionIf the potential difference between the anode and cathode of the X-ray tube is increases
 View Solution
View Solution

