An equilateral triangle is inscribed in the circle with one of the vertices at (a,0). What is the equation of the side opposite to this vertex ?
A
B
C
D
Video Solution
Text Solution
The correct Answer is:C
Since the equilateral is inscribed in the circle with centre at the origin, centroid lies on the origin.
So,
and
So, other vertices of a triangle have coordinates,
and
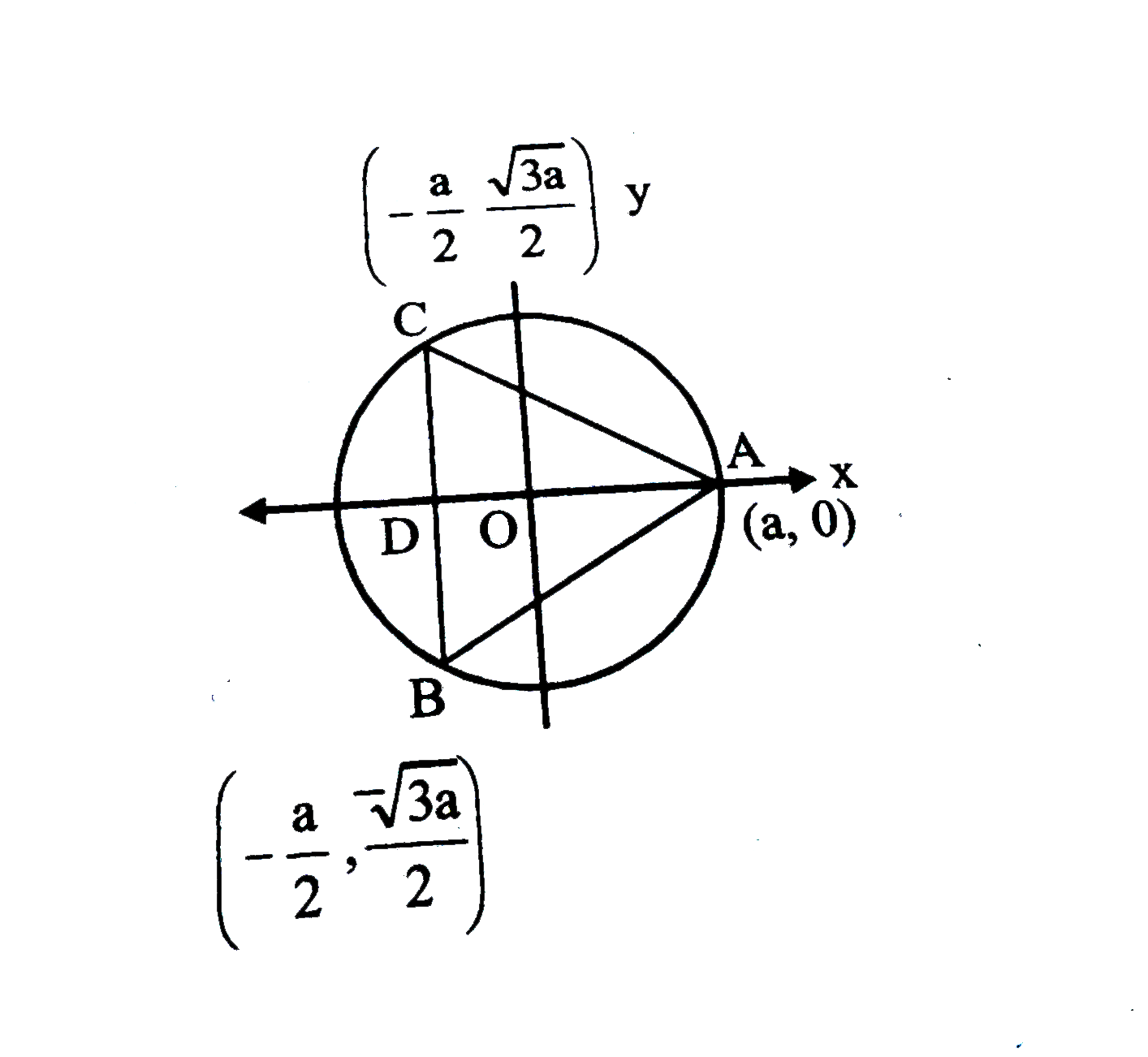
Equation of line is :
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Area of the equilateral triangle inscribed in the circle x2+y2−7x9y+5=0 is
A1558√3squnitsB1658√3squnitsC1758√3squnitsD1858√3squnitsAn equilateral triangle is inscribed in a circle of radius 6 cm. Find its side.
A6√3B6√3C8√3D2√3An equilateral triangle is inscribed in the circle x2+y2=1 which one vertex at the point (1,0). Length of each side of the tringle is
A1B√2C√3/2D√3
If an equilateral triangle is inscribed in a parabola y2=12x with one of the vertices being at the vertex of the parabola then its height
View SolutionIf an equilateral triangle is inscribed in a parabola y2=12x with one of the vertices being at the vertex of the parabola then its height is
View SolutionAn equilateral triangle of side 6 cm is inscribed in a circle. Then radius of the circle is
View SolutionIf an equilateral triangle is inscribed in the circle x2+y2−6x−4y+5=0 then the length of its side
View SolutionAn equilateral triangle of side 9 cm is inscribed in a circle. Find the radius of the circle.
View Solution
