The two circles x2+y2=r2 and x2+y2−10x+16=0 intersect at two distinct points. Then
A
2<r<8
B
r=2 or r=8
C
r<2
D
r>2
Video Solution
Text Solution
The correct Answer is:A
For the circle , x2+y2=r2 centre (0,0) radius =r
If the circle x2+y2−10x+6=0 is compared with general form .
x2+y2+2g+2fy+c=0 ,we get
2g=−10,2f=0,c=16
⇒g=−5,f=0
∴ Centre =(+5,10)
radius =√g2+f2−c=√25+0−16=√9=3.
Given, two circles intersect at two distinct points.
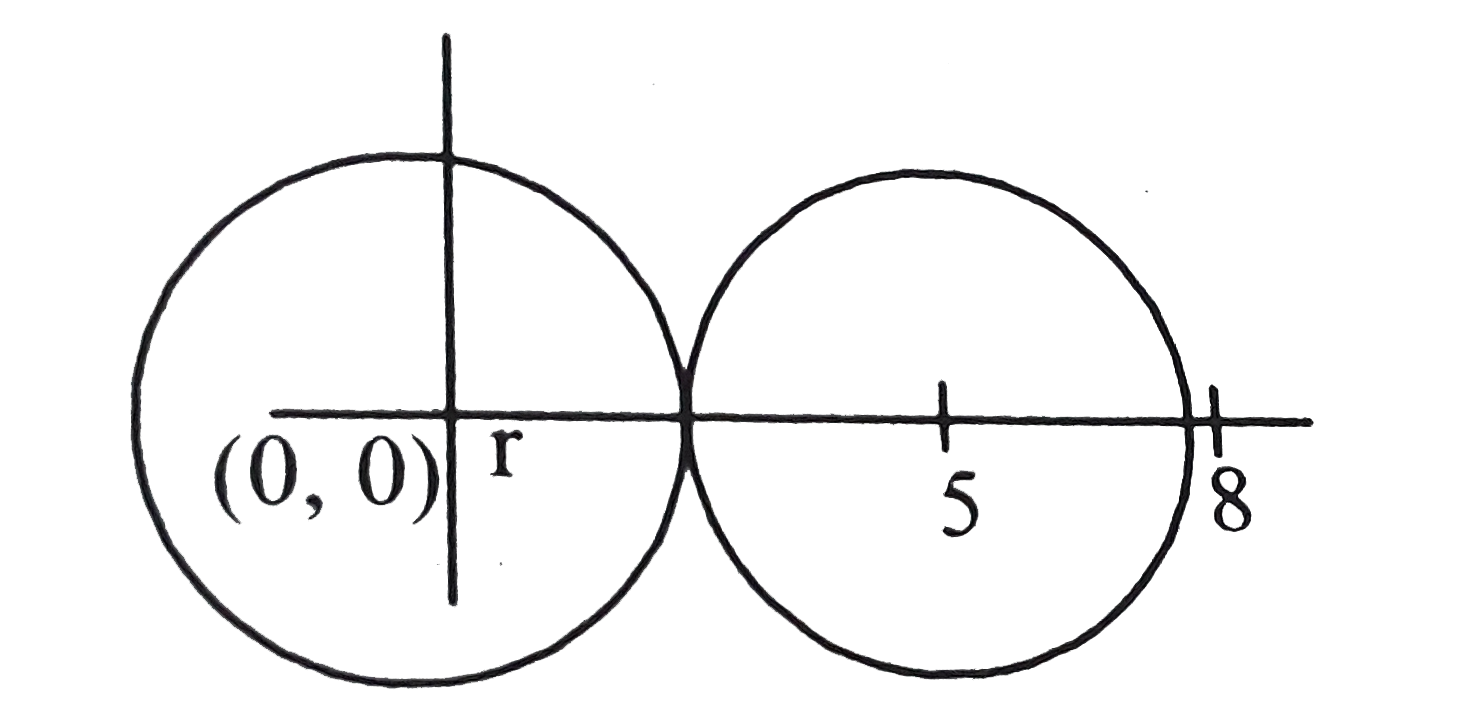
To interset at two points , r should be greater than 2
So, 2<r<8
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The two circle x2+y2=r2 and x2+y2−10x+16=0 intersect at two distinct points . Then which one of the following is correct ?
A2<r<8Br=2 or r = 8Cr<2Dr>2If the circles x2+y2−4x−4y=0 and x2+y2−16=0 intersect in two distinct points P and Q the then line 5x+by−a=0 passes through P and Q for :
Ainfinitely many values of aBexactly two values of aCexactly one value of aDno value of aThe circles x2+y2−10x+16=0andx2+y2=a2 intersect at two distinct point if
Aa<2B2<a<8Ca>8Da=2
The circles x2+y2−10x+16=0 and x2+y2=r2 intersect each other at two distinct points, if
View SolutionIf two circles (x−1)2+(y−3)2=r2 and x2+y2−8x+2y+8=0 intersect in two distinct points , then
View SolutionIf two circles (x−1)2+(y−3)2=r2 and x2+y2−8x+2y+8=0 intersect in two distinct points , then
View SolutionIf two circles (x−1)2+(y−3)2=r2 and x2+y2−8x+2y+8=0 intersect in two distinct points , then
View SolutionThe circles x2+y2+x+y=0 and x2+y2+x−y=0 intersect at an angle of
View Solution
