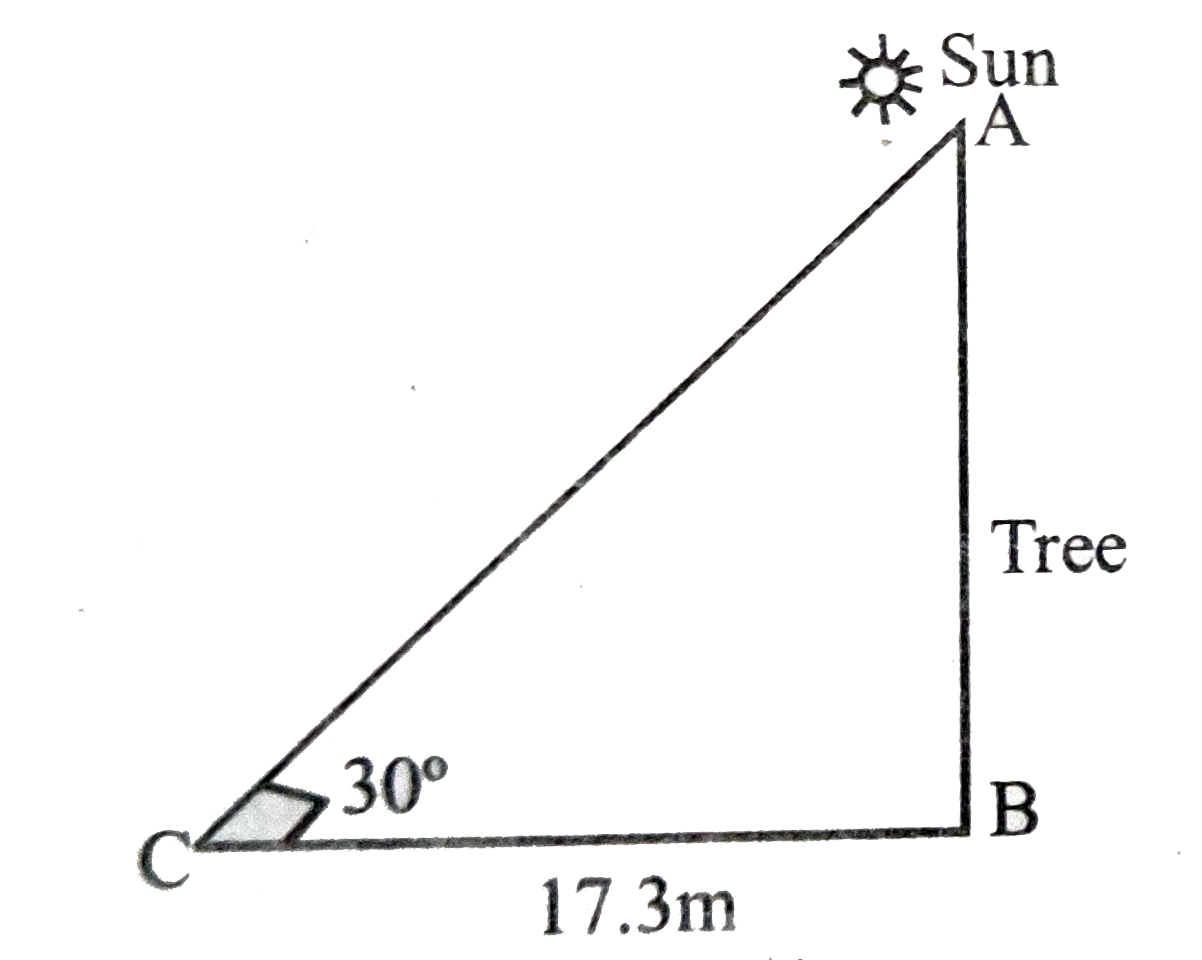
When the sun is 30^@ above the horizon, shadow of one tree is 17.3 m l

The shadow of a tree is 16 meter when elevation of Sun is $60^{\circ}$ . What is the height of the tree ?
A8 m
B16 m
C $16 \sqrt{3}$ m
D $\frac{16}{\sqrt{3}}$ m
A pile driven into the bottom of a lake extends $3 m$ above the bottom of a lake and $1 m$ above the surface of water $(._{a} μ_{ω}) = 4 / 3$ . If the sun is $30^{\circ}$ above the horizon, then the length of the shadow of the pile on the bottom is approximately
A $1.73 m$
B $2.73 m$
C $3.00 m$
D $3.46 m$
The angles of elevation of the top of a building from the top and bot tom of a tree are $30^{\circ} and 60^{\circ}$ respectively .If the height of the tree is 50 m , then what is the height of the building ?
A $50 \sqrt{} 3$
B $75$
C $50 (\sqrt{} 3 + 1)$
D $75 \sqrt{} 3$

When the sun is $30^{\circ}$ above the horizon, shadow of one tree is 17.3 m long What is the height of this tree ?