Using lens maker's formula, derive the thin less formula $\frac{1}{f} = \frac{1}{v} - \frac{1}{u}$ for a biconevex lens.

Text Solution

Verified by Experts

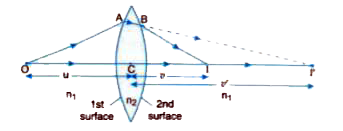
Consider a point object O situated on the principal axis of a bloonvex lens, whose two surfaces have radii of curvature $R_{1} and R_{2}$ respectively. As shown in figure due to refraction at 1st surface of lens an image!. is formed for the object of OC = u,Cl. = v., then using the refraction formula at a single spherical surface, we have
$\frac{n_{2}}{v .} - \frac{n_{1}}{u} = \frac{n_{2} - n_{1}}{R_{1}}$
The image I. behaves as a virtual object for refraction at the second surface of the lens and the final real image is formed at I. Thus, for second surface applying refraction formula, we have
$\frac{n_{1}}{v} - \frac{n_{2}}{v .} = \frac{n_{1} - n_{2}}{R_{2}} = \frac{n_{2} - n_{1}}{(- R_{2})}$
Addng (i) and (ii), we have
$\frac{n_{1}}{v} - \frac{n_{1}}{u} = (n_{2} - n_{1}) (\frac{1}{R_{1}} - \frac{1}{R_{2}})$

$= (n_{21} - 1) (\frac{1}{R_{1}} - \frac{1}{R_{2}})$
However, we know that as per lens maker.s formula
$\frac{1}{f} = (n_{21} - 1) (\frac{1}{R_{1}} - \frac{1}{R_{2}})$
Comparing (iii) and (iv), we get the thin lens formula $\frac{1}{f} = \frac{1}{v} - \frac{1}{u}$

Updated on:21/07/2023

|

Class 12 PHYSICS QUESTION BANK

Similar Questions

Knowledge Check

Lens maker's formula is applicable to
AThin lenses and paraxial rays which subtend very small angles with the principal axis
BThick lenses and paraxial rays which subtend very small angels with the principles axis
CThin lenses and for marginal rays
DThick lenses and for marginal rays

Recommended Questions

Home
Ask Doubt
Profile