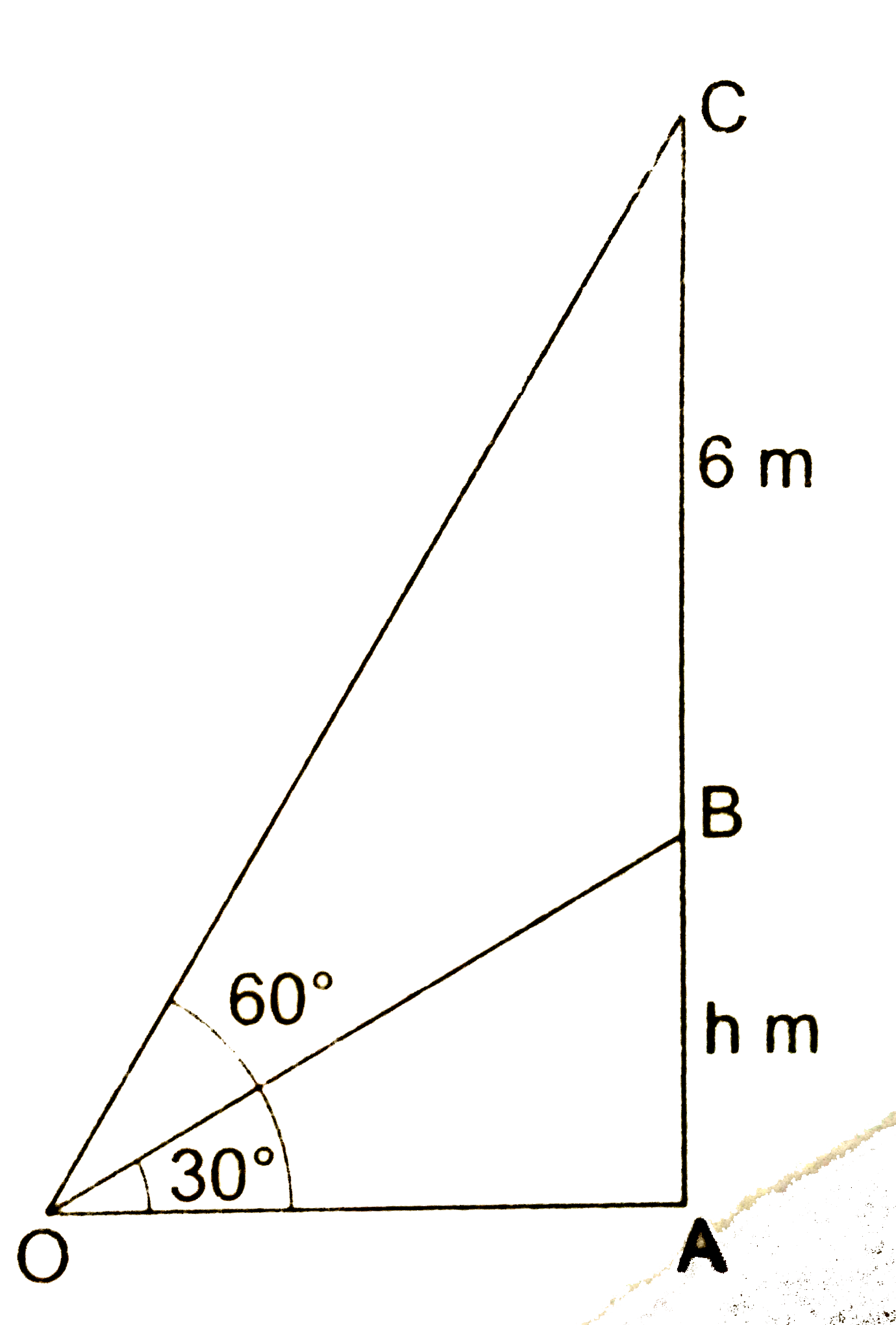
A vertical tower stands on a horizontal plane and is surmounted by vertical flagstaff to height 6m. At a point on the plane, the anglea elevation of the bottom of flagsteff is $30^{\circ}$ and that of the top of the flagstaff is $60^{\circ}$ . Find the height of the tower. [Use $\sqrt{3} = 1.732$ ]

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $3 m$

$\frac{O A}{A B} = {cot 30}^{\circ} \Rightarrow \frac{O A}{h m} = \sqrt{3} \Rightarrow O A = h \sqrt{3} m \dots\dots.. (i)$
$\frac{O A}{A C} = {cot 60}^{\circ} \Rightarrow \frac{O A}{(h + 6) m} = \frac{1}{\sqrt{3}} \Rightarrow O A = \frac{(h + 6)}{\sqrt{3}} m \dots\dots\dots (i i)$
$∴ h \sqrt{3} = \frac{(h + 6)}{\sqrt{3}} \Rightarrow 3 h = h + 6$ .
$\Rightarrow 2 h = 6 \Rightarrow h = 3$ .

|

Updated on:21/07/2023

Class 10 MATHS SOME APPLICATIONS OF TRIGONOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A vertical tower stands on a horizontal plane and surmounted by a flagstaff of height 'h'. At a point on the plane. The angle of elevation of bottom of the flagstaff is $α$ and that of the top of the flagstaffis $β$ . Find the height of the tower :
A $h tan α$
B $\frac{h tan α}{tan β - tan α}$
C $\frac{h tan α}{tan α - tan β}$
DNone of these
Question 2 - Select One
A vertical tower stands on a horizontal plane and surmounted by a flagstaff of height 'h'. At a point on the plane. The angle of elevation of bottom of the flagstaff is $α$ and that of the top of the flagstaffis $β$ . Find the height of the tower :
A $h tan α$
B $\frac{h tan α}{tan α - tan β}$
C $\frac{h tan α}{tan β - tan α}$
D $\frac{tan α + tan β}{h tan α}$

RS AGGARWAL-HEIGHTS AND DISTANCES-Exercise 14

Home
Ask Doubt
Profile