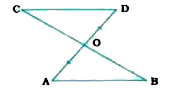
In the given figure , AB||CD . Prove that △AOB~△DOC.

Video Solution
Text Solution
ΔAOB~ΔDOC.
So, the given triangles are equiangular.
∴∠OAB=∠ODC
But, these are alternate angels.
∴AB∣∣CD.
|
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - SOLVED EXAMPLE
4 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE 7 A
1 Videos
- T-RATIOS OF SOME PARTICULAR ANGLESBOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 11
27 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
Similar Questions
Knowledge Check
In the given figure , AB∣∣CD. Find x.
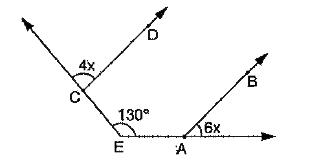 A26∘B13∘C23∘D46∘
A26∘B13∘C23∘D46∘In the figure, AB||CD then
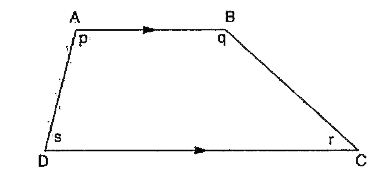 Ap+r=q+sBp−r=q−sCp+s=q+rDp−q=s−r
Ap+r=q+sBp−r=q−sCp+s=q+rDp−q=s−r
In the given figure if AC=BD then prove that AB=CD
View SolutionLine segment AB is parallel to another line segment CD. O is the midpoint of AD (see the given figure). Show that
(i) △AOB=△DOC
(ii) O is also the midpoint of BC
View SolutionIn the given figure, AB∣∣CD. Find the value of x.

View SolutionIn the given figure, AB∣∣CD. Find the value of x.

View SolutionIn the given figure, AB∣∣CD. Find the value of x.

View SolutionIn given figure, show that AB || CD
View Solution

