Prove that the area of equilateral triangle described on the side of a square is half the area of the equilateral triangle described on its diagonal.
GIVEN A ΔABC in which ∠ABC=90∘andAB=BC.ΔABDandΔCAE are equilateral triangles.
TO PROOF ar(ΔABD)=12×ar(ΔCAE)
PROOF Let AB=BC=x units.
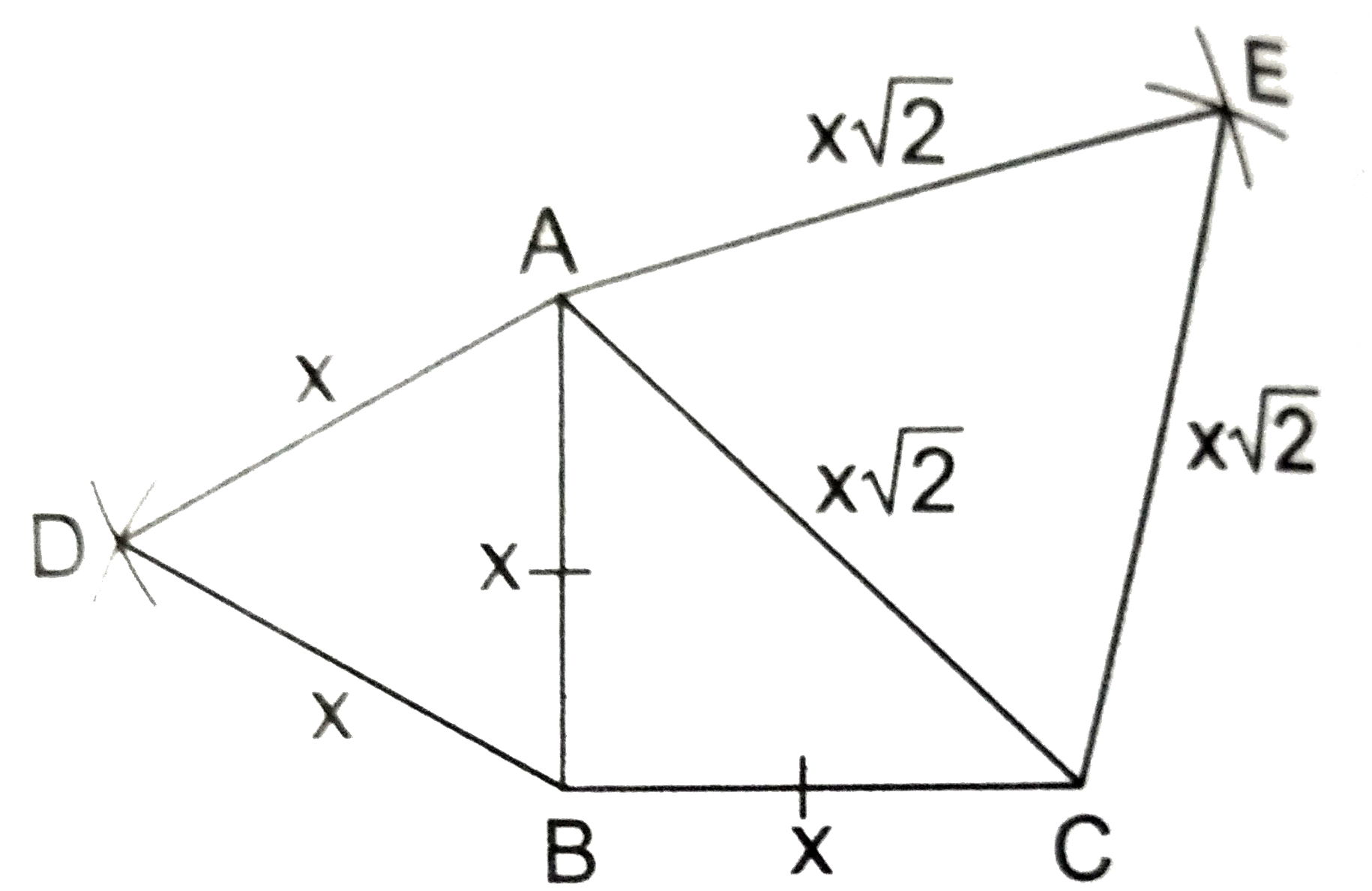
∴hyp.CA=√x2+x2=x√2. units
Each of the ΔABDandCAE being equilateral, each angle of each one of them is 60∘
∴ΔABD~ΔCAE[ by AAA- similarity]
But, the ratio of the areas of two similar triangles is equal to the ratio of the sequare sof their corresponding sides.
∴ar(ΔABD)ar(ΔCAE)=AB2CA2=x2(x√2)2=x22x2=12
Hence, ar(ΔABD)=12×ar(ΔCAE)
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - SOLVED EXAMPLE
4 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE 7 A
1 Videos
- T-RATIOS OF SOME PARTICULAR ANGLESBOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 11
27 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
Similar Questions
Prove that the area of the equilateral triangle described on the side of a square is half the area of the equilateral triangle described on its diagonal.
View SolutionProve that the area of the equilateral triangle described on the side of a square is half the area of the equilateral triangle described on its diagonal.
View Solution
Knowledge Check
Fill in the blanks .
(i) In two similar triangles , ABC and PQR , if their corresponding altitudes AD and PS are in the ratio 4 : 9 , then ar(ΔABC):ar(ΔPQR)=¯¯¯¯¯¯(P) .
(ii) Area of an equilateral triangle described on the side of a square is ¯¯¯¯¯¯(O) the area of equilateral triangle described on its diagonal .
(iii) The altitude of an equilateral triangle with side 'a' equals oberline((R ))APQR16:81Twicea2BPQR4:9Half2aCPQR16:81Half√3a2DPQR4:9Twice√3a2the area of an equilateral triangle is .
A√34a2sq unitsB2a2 sq unitsC3√3a2 sq unitsD√32a2 sq unitsThe area of an equilateral triangle of side 20 cm is
A100√3cm2B100√3cm2C100√32cm2D100√34cm2
Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
View SolutionArea of an equilateral triangle
View SolutionProve that area of an equilateral triangle formed on one side of a given square is one half of area of equilateral triangle formed on diagonal is the same square.
View SolutionProve that the area of an equilateral triangle described on a side of a right-angled isosceles triangle is half the area of the equilateral triangle described on its hypotenuse.
View SolutionWhat is the area of an equilateral triangle with side 2cm?
View Solution
