Prove that the area of the semicircle drawn on the hypotenuse of a right-angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle
GIVEN AΔABC in which ∠B=90∘. Equilateral triangles ΔBCD,ΔCAEandΔABF are drawn on the sides BC, CA and AB respectively.
TO PROOVE ar(ΔCAE)=ar(ΔBCD)+ar(ΔABC)
PROOF ΔBCD,ΔCAEandΔABF are equiangular and hence similar.
We have
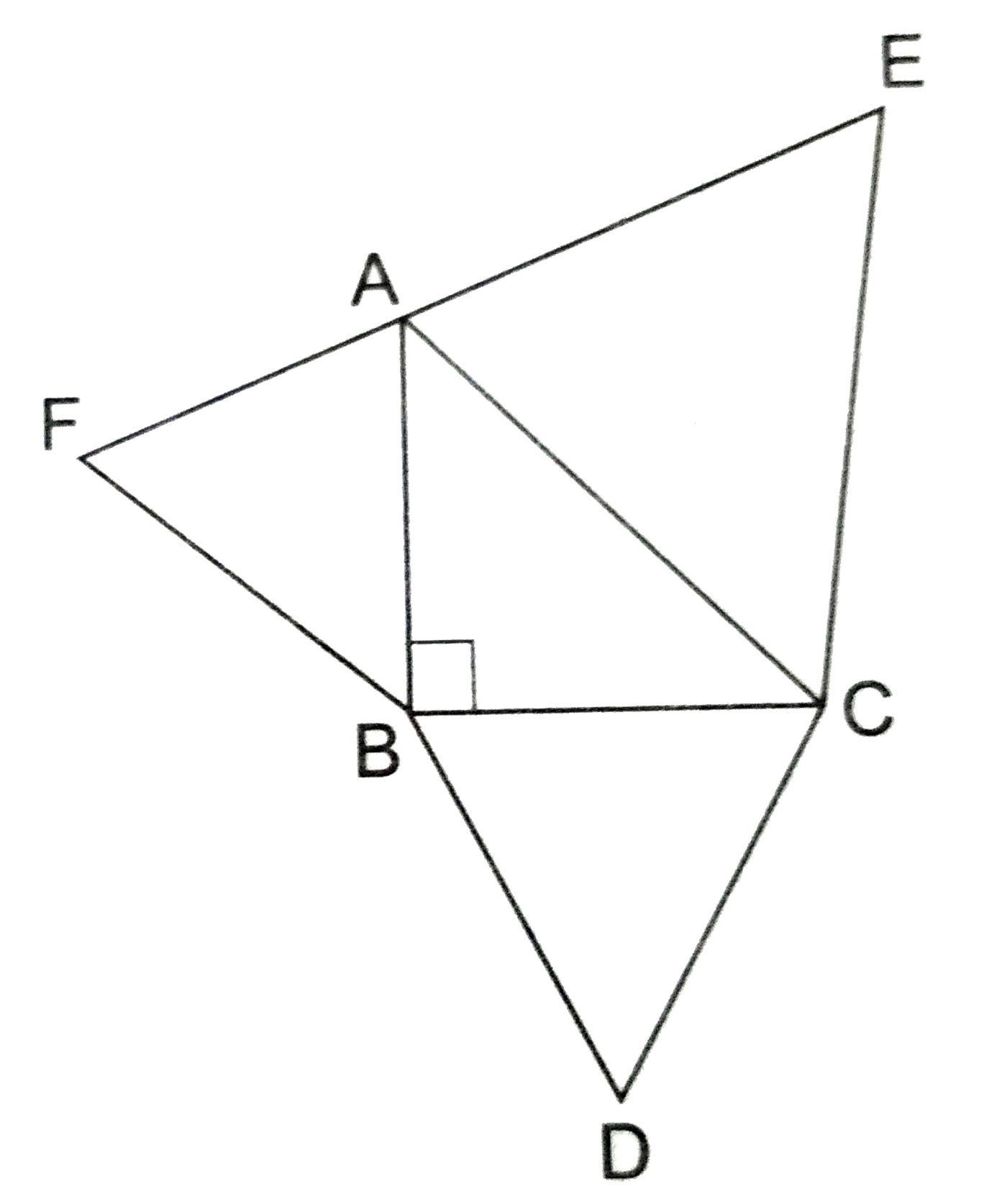
ar(ΔBCD)ar(ΔCAE)+ar(ΔABF)ar(ΔCAE)=BC2CA2+AB2CA2
⇒ar(ΔBCD)+(ΔABF)ar(ΔCAE)=BC2+AB2CA2=CA2CA2=1 [ by Pythagora's theorem]
⇒ar(ΔBCD)+ar(ΔABF)=ar(ΔCAE)
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - SOLVED EXAMPLE
4 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE 7 A
1 Videos
- T-RATIOS OF SOME PARTICULAR ANGLESBOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 11
27 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
Similar Questions
Prove that the area of the equilateral triangle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the equilateral triangles drawn on the other two sides of the triangle.
View SolutionThe length of the two sides of a right-angled triangle are equal Find the length of the hypotenuse
View Solution
Knowledge Check
The hypotenuse of a right-angled isosceles triangle is 5 cm. The area of the triangle is (a) 5 cm2 (b) 6.25 cm2 (c) 6.5 cm2 (d) 12.5 cm2
A5 cm2B6.25 cm2C6.5 cm2D12.5 cm2
Prove that, in a right-angled triangle, the square of hypotenuse is equal to the sum of the square of remaining two sides.
View SolutionIf the length of the hypotenuse of a right angled triangle is 10 cm, then what is the maximum area of such a right angled triangle?
View SolutionEquilateral triangles are drawn on the sides of a right triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.
View SolutionProve that is a right angle triangle, the square of the hypotenuse is equal the sum of the squares of other two sides.
View SolutionTheorem 6.8 : In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
View SolutionProve that the area of right-angled triangle of given hypotenuse is maximum when the triangle is isosceles.
View SolutionThe hypotenuse of a right-angled triangle is 10 cm and its area is 24 cm2. If the shorter side is halved and the longer side is doubled, the new hypotenuse becomes
View Solution
