सिद्ध करें कि कोई धन पूर्णांक 6k या 6k + 1 या 6k+2 या 6k + 3 या 6k +4 या 6k +5 के रूप में लिखा जा सकता है।
Step by step video & image solution for सिद्ध करें कि कोई धन पूर्णांक 6k या 6k + 1 या 6k+2 या 6k + 3 या 6k +4 या 6k +5 के रूप में लिखा जा सकता है। by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - ALOK BHARTI PUBLICATIONCHAPTER - गणितEXERCISE - बीजगणित : 20 अंक153videos
गणित
- BOOK - ALOK BHARTI PUBLICATIONCHAPTER - गणितEXERCISE - त्रिकोणमिति : 12 अंक77videos
गणित
- BOOK - ALOK BHARTI PUBLICATIONCHAPTER - गणितEXERCISE - सांख्यिकी एवं प्रायिकता : 11 अंक51videos
गणित
- BOOK - ALOK BHARTI PUBLICATIONCHAPTER - झारखण्ड माध्यमिक बोर्ड परीक्षा (गणित)EXERCISE - 2009-(खण्ड - .द.)7videos
झारखण्ड माध्यमिक बोर्ड परीक्षा (गणित)
Similar Questions
किसी बहुपद p(x) के लिए, y = p(x) का ग्राफ नीचे आकृति में दिया गया है, p(x) के शून्यकों की संख्या लिखें।
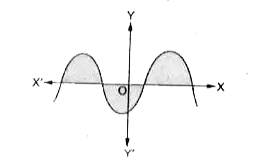 00:57View Solution
00:57View Solutionयदि secθ=1312 हो, तो अन्य सभी त्रिकोणमितीय अनुपात परिकलित कीजिए।
07:21View Solutionनिम्न आँकड़ों का माध्य ज्ञात करें
 02:53View Solution
02:53View Solutionद्विघात समीकरण 2x2−6x+3=0 के मूलों की प्रकृति ज्ञात कीजिए | यदि वास्तविक मूलों का अस्तित्व हो, तो उन्हें ज्ञात कीजिए |
01:53View Solution-1=(6k-3)/(k+1)
02:34View SolutionIf cos3x+sin(2x−7π6)=−2 , then x is equal to (k∈Z) π3(6k+1) (b) π3(6k−1) π3(2k+1) (d) none of these
01:40View SolutionThe unit vector parallel to the internal angle bisector of the vectors 2i+3i+6k and 2i-3j-6k is
02:50View SolutionPairs of numbers of the form (6k-1) and (6k+1) are twin primes.Is this statement true?
01:59View SolutionIf (k-1),(2k+1),(6k+3) are in GP then k=?
05:26View SolutionPairs of numbers of the form (6k−1) and (6k+1) are twin primes. Is this statement true ?
03:26View Solutionसिद्ध करें कि कोई धन पूर्णांक 6k या 6k+1 या 6k+2 या 6k+3 या 6k+4 या 6k+5 के रूप में लिखा जा सकता है।
01:44View Solution2 और 3 के अतिरिक्त कोई अभाज्य संख्या अवश्य ही 6k+1 या …….. रूप का होगा।
02:43View SolutionIf ¯a is collinear with ¯b=3i + 6j + 6k and ¯a.¯b=27, then ¯a=
04:11View SolutionIf the vector a = 2i + 3j + 6k and b are collinear and |b| = 21, then b =
02:36View SolutionFor what value of m ,the vector A=2i∧+3j∧−6k∧ is perpendicular to vector B=3i∧−mj∧+6k∧
02:55View SolutionIf F=2i+3j−kandr=i−j+6k find rx F
02:57View Solution

