An iron bar of length L, cross-section area A and Young's modulus Y is pulled by a force F from both ends so as to produce an elongation l . Which of the following statements is correct?
The correct Answer is:B
To solve the problem, we need to analyze the relationship between the force applied to the iron bar, its elongation, cross-sectional area, and Young's modulus.
1. Understanding Young's Modulus:
Young's modulus (Y) is defined as the ratio of longitudinal stress to longitudinal strain. Mathematically, it can be expressed as:
Y=StressStrain
where:
- Stress = FA (Force per unit area)
- Strain = ΔLL (Change in length per original length)
2. Expressing Stress and Strain:
- Stress can be calculated as:
Stress=FA
- Strain can be expressed as:
Strain=lL
where l is the elongation and L is the original length of the bar.
3. Substituting Stress and Strain into Young's Modulus:
Substituting the expressions for stress and strain into the formula for Young's modulus, we get:
Y=FAlL=F⋅LA⋅l
4. Rearranging the Equation:
Rearranging the equation gives us:
F=Y⋅A⋅lL
This shows that the force F is directly proportional to the elongation l and Young's modulus Y, and inversely proportional to the length L and the cross-sectional area A.
5. Analyzing the Relationship:
From the rearranged equation, we can conclude that:
- If the cross-sectional area A increases, the force F required to produce the same elongation l decreases.
- If the length L increases, the force F required to produce the same elongation l also decreases.
6. Conclusion:
The correct statement is that the elongation l is inversely proportional to the cross-sectional area A of the bar, given a constant force F and Young's modulus Y.
Young's modulus (Y) is defined as the ratio of longitudinal stress to longitudinal strain. Mathematically, it can be expressed as:
Y=StressStrain
where:
- Stress = FA (Force per unit area)
- Strain = ΔLL (Change in length per original length)
- Stress can be calculated as:
Stress=FA
- Strain can be expressed as:
Strain=lL
where l is the elongation and L is the original length of the bar.
Substituting the expressions for stress and strain into the formula for Young's modulus, we get:
Y=FAlL=F⋅LA⋅l
Rearranging the equation gives us:
F=Y⋅A⋅lL
This shows that the force F is directly proportional to the elongation l and Young's modulus Y, and inversely proportional to the length L and the cross-sectional area A.
From the rearranged equation, we can conclude that:
- If the cross-sectional area A increases, the force F required to produce the same elongation l decreases.
- If the length L increases, the force F required to produce the same elongation l also decreases.
The correct statement is that the elongation l is inversely proportional to the cross-sectional area A of the bar, given a constant force F and Young's modulus Y.
Topper's Solved these Questions
- BULK PROPERTIES OF MATTERBook:MTG-WBJEEChapter:BULK PROPERTIES OF MATTERExercise:WB JEE WORKOUT (ONE OR MORE THAN ONE OPTION CORRECT TYPE )
Explore 10 Videos
- BULK PROPERTIES OF MATTERBook:MTG-WBJEEChapter:BULK PROPERTIES OF MATTERExercise:WB JEE PREVIOUS YEARS QUESTIONS (SINGLE OPTION CORRECT TYPE)
Explore 22 Videos
- ATOMS MOLECULES AND CHEMICAL ARITHEMETIC Book:MTG-WBJEEChapter:ATOMS MOLECULES AND CHEMICAL ARITHEMETIC Exercise:WB JEE PREVIOUS YEARS QUESTIONS CATEGORY 1: SINGLE OPTION CORRECT TYPE (1 MARK)
Explore 3 Videos
- CURRENT ELECTRICITY Book:MTG-WBJEEChapter:CURRENT ELECTRICITY Exercise:WB JEE PREVIOUS YEARS QUESTIONS
Explore 21 Videos
Similar Questions
A smooth uniform, string of natural length l, cross-sectional area A and Young’s modulus Y is pulled along its length by a force F on a horizontal surface. Find the elastic potential energy stored in the string.
View SolutionA uniform rod of length cross- sectional area A and Young's modulus Y is subjected to two forces F and 2F at its two ends, stretching the rod.The heat generated in the rod is found to be (10a+b)F2l12AY .Find a+b.{a,b : Positive integers}
View Solution
Knowledge Check
An iron bar of length l cross section 'A' and young's modulus Y is pulled by a force F from both ends so as to produce an elongation 'e'. Which of the following statements is correct?
Ae∝YBe∝ACe∝lADe∝1lA uniform cylindrical rod of length L, cross-section area A and Young's modulus Y is acted upon by the force as shown in Fig. 7(CF).3. The elongation of the rod is
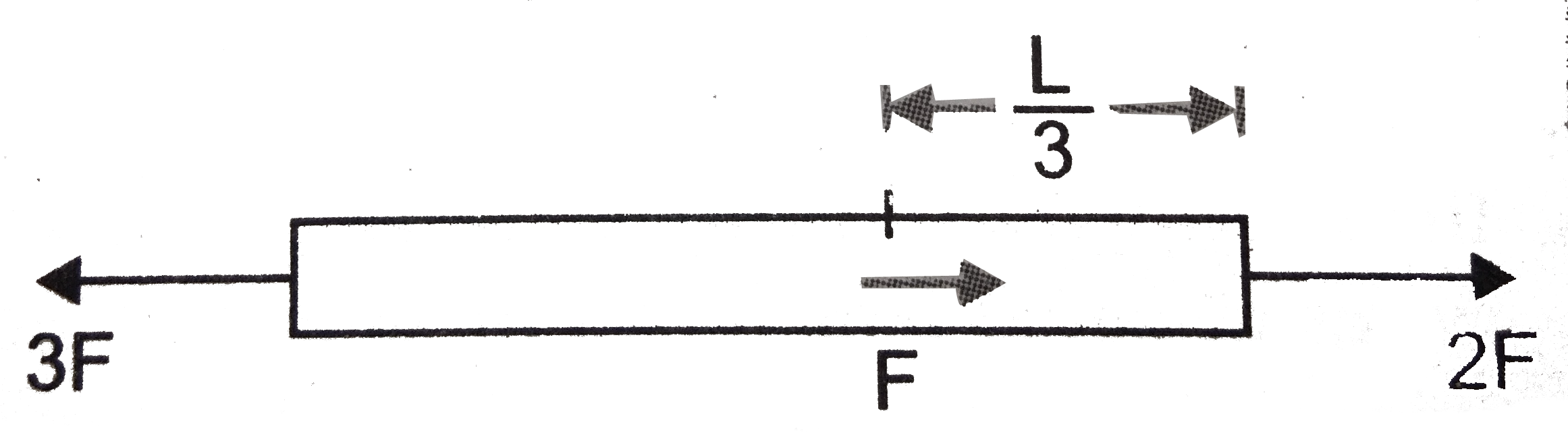 A2FL5AYB3FL5AYC3FL8AYD8FL3AY
A2FL5AYB3FL5AYC3FL8AYD8FL3AYA smooth uniform string of natural length L0, cross-sectional area A and Young's modulus Y is pulled along its length by a force F on a horizontal smooth surface. The elastic potential energy stored in the string is
A2F2L0AYBF2L02AYCF2L02AYDF2L06AY
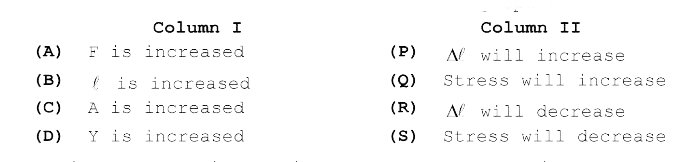
A wire of length l, area of cross section A and Young’s modulus of elasticity Y is stretched by a longitudinal force F. The change in length is Δl Match the following two columns.
View SolutionA metal wire of length L, area of cross-section A and Young's modulus Y behaves as a spring of spring constant k.
View SolutionThe length of an iron wire is L and area of cross - section is A. The increase of length l is observed on applying the force F on its two ends. Which of the following statement is correct ?
View SolutionA metal wire of length L, area of cross-section A and young's modulus Y is stretched by a variable force F such that F is always slightly greater than the elastic forces of resistance in the wire. When the elongation of the wire is l
View SolutionA mass (m) is suspended at the end of a weightless wire of length L, cross-sectional area A and Young's modulus Y. The period of oscillation for the S.H.M. along the vertical direction is
View Solution