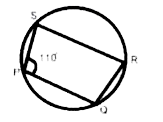
PQRST is cyclic pentagon and PT is a diameter, then ∠(PQR)+∠RST is equal to
180∘
270∘
216∘
144∘
The correct Answer is:B
To solve the problem, we need to find the sum of angles ∠PQR and ∠RST in the cyclic pentagon PQRST where PT is a diameter.
1. Understanding the Cyclic Pentagon:
A cyclic pentagon is a five-sided figure where all vertices lie on a single circle. The angles subtended by the same arc are equal.
2. Using the Property of Cyclic Quadrilaterals:
Since PT is a diameter, by the inscribed angle theorem, the angles subtended by the diameter at any point on the circle are right angles. Therefore, ∠PQR and ∠RST can be analyzed using this property.
3. Finding the Sum of Interior Angles of the Pentagon:
The sum of the interior angles of a pentagon is given by the formula:
Sum of interior angles=(n−2)×180∘
where n is the number of sides. For a pentagon, n=5:
Sum=(5−2)×180∘=3×180∘=540∘
4. Analyzing the Angles:
Since PT is a diameter, we know:
∠PQR+∠RST=90∘+90∘=180∘
However, we need to find the specific values of ∠PQR and ∠RST.
5. Using the Equal Angles Property:
In a cyclic pentagon, if we assume that the angles ∠PQR and ∠RST are equal due to symmetry (as PQ=QR=RS=ST), we can denote:
∠PQR=xand∠RST=x
Therefore, we have:
x+x=180∘⟹2x=180∘⟹x=90∘
6. Final Calculation:
Thus, the sum of the angles ∠PQR+∠RST is:
∠PQR+∠RST=90∘+90∘=180∘
Conclusion:
The sum of the angles ∠PQR+∠RST is 180∘.
A cyclic pentagon is a five-sided figure where all vertices lie on a single circle. The angles subtended by the same arc are equal.
Since PT is a diameter, by the inscribed angle theorem, the angles subtended by the diameter at any point on the circle are right angles. Therefore, ∠PQR and ∠RST can be analyzed using this property.
The sum of the interior angles of a pentagon is given by the formula:
Sum of interior angles=(n−2)×180∘
where n is the number of sides. For a pentagon, n=5:
Sum=(5−2)×180∘=3×180∘=540∘
Since PT is a diameter, we know:
∠PQR+∠RST=90∘+90∘=180∘
However, we need to find the specific values of ∠PQR and ∠RST.
In a cyclic pentagon, if we assume that the angles ∠PQR and ∠RST are equal due to symmetry (as PQ=QR=RS=ST), we can denote:
∠PQR=xand∠RST=x
Therefore, we have:
x+x=180∘⟹2x=180∘⟹x=90∘
Thus, the sum of the angles ∠PQR+∠RST is:
∠PQR+∠RST=90∘+90∘=180∘
The sum of the angles ∠PQR+∠RST is 180∘.
Similar Questions
Knowledge Check
PQRST is a cyclic pentagon and PT is a diameter, then ∠PQR+∠RST is equal to the
A180∘B270∘C216∘D144∘PQRS is a cyclic quadrilateral and PQ is the diameter of circle . If ∠RPQ=38∘ , what is the value (in degrees) of ∠PSR ?
A52B77C128D142In Δ PQR,PS is the bisector of ∠PandPT⊥QR, where ∠ Q = 60 and ∠R = 30 then ∠TPS is equal to
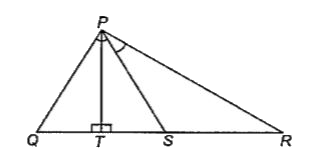 A10B30C60D15
A10B30C60D15
PQRS is a cyclic quadrilateral. If angle P is four times the ∠R and ∠S is three times the ∠Q , then the sum of ∠Q and ∠R is:
PQRS एक चक्रीय चतुर्भुज है | यदि कोण P कोण R से चार गुना है तथा कोण S कोण Q से तीन गुना है, तो कोण Q और R का योग ज्ञात करें |
View SolutionIn the given figures, PQRS is a cyclic quadrilateral. What is the measure of the ∠PQR, if PQ is parallel to the SR?
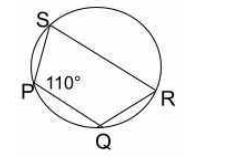
View SolutionIn the figure, O is the centre of the circle . ∠PQR is equal to
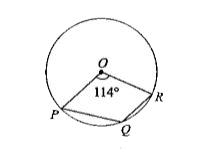
View SolutionPQRs is a cyclic quadrilateral. Find the measure of ∠Pand∠Q.
View SolutionABCD is a cyclic parallelogram. The angle ∠B is equal to :
View Solution