If PQ and PR be the two tangents to a circle with centre O such that ∠QPR=120∘ then ∠POQ is
90∘
45∘
30∘
60∘
The correct Answer is:C
To solve the problem, we need to find the angle ∠POQ given that ∠QPR=120∘ and PQ and PR are tangents to a circle with center O.
1. Draw the Diagram:
- Start by drawing a circle with center O.
- Mark a point P outside the circle from which two tangents PQ and PR are drawn to the circle, touching it at points Q and R respectively.
2. Identify the Angles:
- Since PQ and PR are tangents to the circle, the angles ∠OPQ and ∠OPR are both 90∘ (tangent to radius).
- We know ∠QPR=120∘.
3. Use Triangle Properties:
- In triangle PQR, we can find the angles ∠PQR and ∠PRQ using the fact that the sum of angles in a triangle is 180∘:
∠PQR+∠PRQ+∠QPR=180∘
- Let ∠PQR=∠PRQ=x. Thus, we have:
x+x+120∘=180∘
2x=60∘⟹x=30∘
- Therefore, ∠PQR=30∘ and ∠PRQ=30∘.
4. Find ∠POQ:
- Now, consider triangle POQ:
- We know ∠OPQ=90∘ and ∠PQR=30∘.
- The angle ∠POQ can be found using the triangle angle sum property:
∠POQ+∠OPQ+∠PQR=180∘
∠POQ+90∘+30∘=180∘
∠POQ+120∘=180∘
∠POQ=180∘−120∘=60∘
Final Answer:
Thus, ∠POQ=60∘.
- Start by drawing a circle with center O.
- Mark a point P outside the circle from which two tangents PQ and PR are drawn to the circle, touching it at points Q and R respectively.
- Since PQ and PR are tangents to the circle, the angles ∠OPQ and ∠OPR are both 90∘ (tangent to radius).
- We know ∠QPR=120∘.
- In triangle PQR, we can find the angles ∠PQR and ∠PRQ using the fact that the sum of angles in a triangle is 180∘:
∠PQR+∠PRQ+∠QPR=180∘
- Let ∠PQR=∠PRQ=x. Thus, we have:
x+x+120∘=180∘
2x=60∘⟹x=30∘
- Therefore, ∠PQR=30∘ and ∠PRQ=30∘.
- Now, consider triangle POQ:
- We know ∠OPQ=90∘ and ∠PQR=30∘.
- The angle ∠POQ can be found using the triangle angle sum property:
∠POQ+∠OPQ+∠PQR=180∘
∠POQ+90∘+30∘=180∘
∠POQ+120∘=180∘
∠POQ=180∘−120∘=60∘
Thus, ∠POQ=60∘.
Similar Questions
Knowledge Check
- Question 1 - Select One
If TP and TQ are two tangents to a circle with centre O, so that ∠POQ=120∘, then ∠PTQ is equal to
A120∘B30∘C60∘D90∘ - Question 2 - Select One
If PQ and PR are two tangents to ta circle with centre O. if ∠QPR=46∘, then ∠QOR is equal to
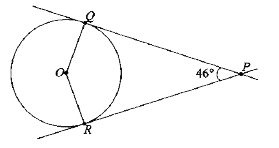 A67∘B46∘C44∘D134∘
A67∘B46∘C44∘D134∘ - Question 3 - Select One
In the figure , PQ and PR are the tangents drawn form P to a circle with centre O. if ∠OPQ=35∘ then
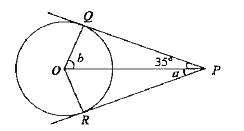 Aa=30∘,b=60∘Ba=35∘,b=55∘Ca=40∘,b=50∘Da=45∘,b=45∘
Aa=30∘,b=60∘Ba=35∘,b=55∘Ca=40∘,b=50∘Da=45∘,b=45∘
Circles 1. If PQ and PR are two tangents to a circle with centre O. If ∠QPR=46∘, find∠QOR
View SolutionIn Fig. 10.101, PQ and PR are two tangents to a circle with centre O . If ∠QPR=46o , then ∠QOR equals (FIGURE) 67o (b) 134o (c) 44o (d) 46o
View SolutionIn figure, PQ and PR are two tangents to a circle with centre O. IF ∠QPR=46∘ , then ∠QOR equals
 View Solution
View SolutionIn Figure 4, PQ and PR are tangents drawn to a circle with centre O from an external point P. If ∠PRQ=70∘, then find ∠QPRand∠OQR
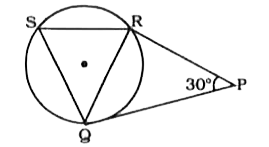
View SolutionIn the given figure tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPO=30∘. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.
 View Solution
View Solution

