Question

Using indifference curve approach , explain the conditions of consumer's equilibrium .

Explanation

(i) To define consumer equilibrium, we use Interference Curve map and the budget line .
Two conditions for consumer Equilibrium
(a) Necessary Condition
Marginal Rate of Substitution = Market Rate of Exchange `[(P_x)/(P_y)]`
Or , `MRS_(x,y)=P_x//P_y`
( Market Rate of Exchange ) MRE
Or `MRS_(x,y) =MRE[(P_x)/P_y]`
`"*" ` If `MRS_(x,y) gt MRE [(P_x)/(P_y)]` ,
At point T in figure
It means the consumer.s willingness to pay for commodity X is higher than what makes values for commodity X. So, the consumer should buy more of X and less of Y to get MRS `=P_x/P_y`

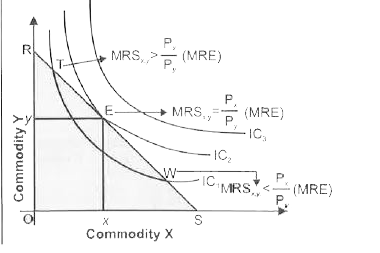
`"*"` If `MRS_(x,y) lt MRE [(P_x)/(P_y)]`, At point W in figure,
It means the consumer willingness to pay for commodity X is lesser than what market value for commodity X ,So, consumer should buy less of X and more Y to get MRS = `p_x/p_y`
(b) Sufficient Condition
`MRS_(x,y)` Diminishing (Convex) at a point of equilibrium i.e., when
`MRS_(xy)=MRE[P_x/P_y]`
(ii) The consumer will reach equilibrium when the budget line is tangential to the higher possible Indifference Curve, i.e. ., where necessary and sufficient condition satisfy . In the above diagram , the consumer will reach equilibrium at point E where budget line RS is tangential to the higher possible `IC_2`
(iii) The consumer cannot move to Indifference Curve , i.e. ., `IC _3` as this is beyond this money income.
(iv) Even on `IC_2` all the other points except E are beyond his means .
(v) Hence , at point E, the consumer is in equilibrium where his satisfaction maximizes, given his income and prices of goods X and Y . In equilibrium at E , the slope of Budget line = the slope of Indifference Curve. Therefore `MRS_(xy)` is equal to the ratio of the price bof two goods `[(P_x)/(P_y)]` .