For non-empty subsets A,B and C of a set X such that A∪B=B∩C, which one of the following, is the strongest inference that can be derived? a)A=B=C b) A⊆B=C c) A=B⊆C d) A⊆B⊆C
A
A=B=C
B
A⊆B=C
C
A=B⊆C
D
A⊆B⊆C
Video Solution
Text Solution
The correct Answer is:D
∵A∪B=B∩C
Since union of A∪B is same as infersection B∩C where ABC are non-empty subsets of X, strongest inference is A⊆B⊆C which can be shown in Venn diagram as below :
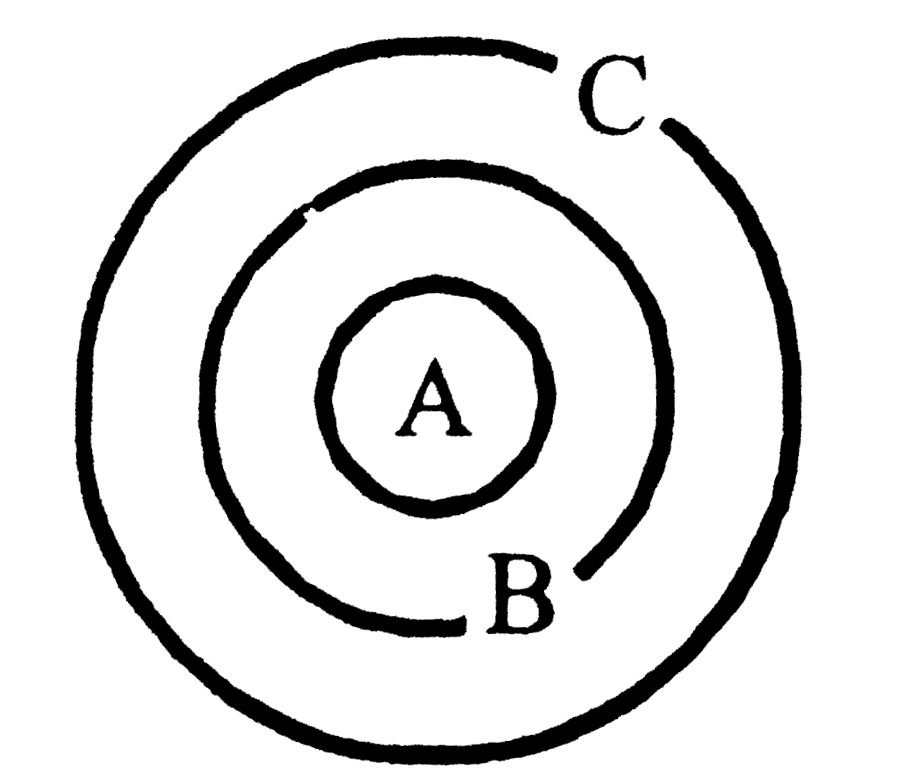
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
For non-empty subsets A,B and C of a set X such that A∪B=B∩C, which one of the following, is the strongest inference that can be derived? a)A=B=C b) A⊆B=C c) A=B⊆C d) A⊆B⊆C
AA=B=CBA⊆B⇒CCA=B⊆CDA⊆B⊆CLet A and B be two non-empty subsets of a set X. If (A−B)∪(B−A)=A∪B, then which one of the following is correct?
AA⊂BBA⊂(X−B)CA=BDB⊂AIf A, B and C Are subsets of a given set, then which one of the following isrelations is not correct?
AA. A∪(A∩B)=A∪BBB. A∩(A∪B)=ACC. (A∩B)∪C=(A∪C)∩(B∪C)DD. (A∪B)∩C=(A∩C)∪(B∩C)
Let A and B be two non-empty subsets of a set X. If (A−B)∪(B−A)=A∪B, then which one of the following is correct?
View SolutionIn the set X = {a, b, c, d}, which of the following functions in X?
View SolutionSuppose a,b,c,d ∈C and let A =[abcd] . Then which one of the following is not true ?
View SolutionLet A and B be two non-empty subsets of a set X such that A is not a subset of B then
View SolutionIf A,B and C be any three sets , then A∪(B∩C) is the same as :
View Solution
