A, B, C and D are four sets such that . Consider the following :
1. and are always disjoint.
2. are always disjoint
Which of the above statements is/are correct ?
1 only
2 only
Both 1 and 2
Neither 1 nor 2
The correct Answer is:B
To solve the problem, we need to analyze the given sets A, B, C, and D based on the conditions provided. Let's break it down step by step.
Given:
- A∩B=ϕ (A intersection B is empty)
- C∩D=ϕ (C intersection D is empty)
Statements to evaluate:
1. A∪C and B∪D are always disjoint.
2. A∩C and B∩D are always disjoint.
Step 1: Analyze Statement 1
- We need to check if A∪C and B∪D are disjoint.
- Since A∩B=ϕ, it means there are no common elements between A and B.
- Since C∩D=ϕ, it means there are no common elements between C and D.
Now, consider the unions:
- A∪C contains all elements from both A and C.
- B∪D contains all elements from both B and D.
Since there are no common elements between A and B, and between C and D, we cannot conclude that A∪C and B∪D are disjoint. For example, if A = {1, 2}, B = {3, 4}, C = {1, 5}, and D = {6, 7}, then:
- A∪C={1,2,5}
- B∪D={3,4,6,7}
Here, they are disjoint. However, if we change C to {3}, then A∪C and B∪D would not be disjoint. Thus, this statement is not always true.
Step 2: Analyze Statement 2
- We need to check if A∩C and B∩D are disjoint.
- Since A∩B=ϕ, it means A and B have no common elements.
- Since C∩D=ϕ, it means C and D have no common elements.
Now, consider the intersections:
- A∩C could potentially have elements from A and C.
- B∩D could potentially have elements from B and D.
Since A and B are disjoint and C and D are disjoint, A∩C and B∩D cannot have any elements in common. Therefore, A∩C and B∩D are always disjoint.
Conclusion:
- Statement 1 is incorrect.
- Statement 2 is correct.
Final Answer:
- Only Statement 2 is correct.
- A∩B=ϕ (A intersection B is empty)
- C∩D=ϕ (C intersection D is empty)
1. A∪C and B∪D are always disjoint.
2. A∩C and B∩D are always disjoint.
- We need to check if A∪C and B∪D are disjoint.
- Since A∩B=ϕ, it means there are no common elements between A and B.
- Since C∩D=ϕ, it means there are no common elements between C and D.
- A∪C contains all elements from both A and C.
- B∪D contains all elements from both B and D.
- A∪C={1,2,5}
- B∪D={3,4,6,7}
- We need to check if A∩C and B∩D are disjoint.
- Since A∩B=ϕ, it means A and B have no common elements.
- Since C∩D=ϕ, it means C and D have no common elements.
- A∩C could potentially have elements from A and C.
- B∩D could potentially have elements from B and D.
- Statement 1 is incorrect.
- Statement 2 is correct.
- Only Statement 2 is correct.
Topper's Solved these Questions
Similar Questions
Consider the following statements :
1. An isosceles trapezium is always cyclic.
2. Any cyclic parallelogram is a rectangle.
Which of the above statements is/are correct?
View Solution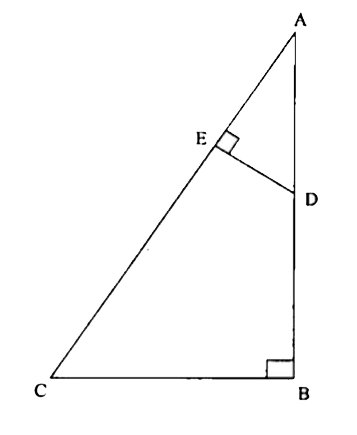
In the figure given above ∠ABC=∠AED=90∘
Consider the following statements :
1. ABC and ADE are similar triangles.
2. The four points B, C,E and D may lie on a circle.
Which of the above statements is/are correct ?
View Solution
Knowledge Check
Consider the following statements
I. sin |x| + cos |x| is always positive
II. sin(x2)+cos(x2) is always positive
Which of the above statement is/are correct?AA) Only IBB) Only IICC) Both I and IIDD) Neither I nor IIFor the reaction
A+B→2C+D which of the following statements is/are correct?ARate of disappearance of B = 1/2 x rate of appearance of CBRate of disappearance of B =1/2 x rate of appearance of CCRate of disappearance of A = rate of appearance of BDRate of disapperance of A = rate of disapperance of B.If A and B are two disjoint sets, then which one of the following is correct?
AA−B=A−(A∩B)BB−A'=A∩BCA∩B=(A−B)∩BDAll of these
The angles A, B,C, D of a quadrilateral ABCD are in the ratio 1:2:4:5.
Consider the following statements :
1. ABCD is a cyclic quadrilateral.
2. sin (B - A) = cos (D - C).
Which of the above statements is/are correct ?
View SolutionConsider the following statements :
1. sin10>1
2. cos1∘<cos1
Which of the above statements is/are correct?
View SolutionConsider the following statements :
1. If f(x)=x2andg(y)=y3 then f=g.
2. Identity function is not always a bijection.
Which of the above statements is/are correct ?
View SolutionConsider the following
1. A∪(B∩C)=(A∩B)∪(A∩C)
II. A∩(B∪C)=(A∪B)∩(A∪C)
Which of the above statement(s) is/are correct?
View SolutionConsider the following statements:
A real image
1. can be formed on a screen
2. is always magnified and inverted
Which of the statements given above is/are correct?
View Solution
