The number of ways of arranging m white and n black balls in a row (m>n) so that no two black are placed together, is
m+1Cn×n!
mCn
m+1Cn
m!n!
Since m>n and we have to find the total number of arrangements of m+n balls so that no two black balls are together. So we first arrange m white balls in a row. This can be done in only one way as all white balls are identical.
Now, we have (m+1) places between m white balls and we want that no two black balls are together. So, we select n places out of (m+1) and then arrange them in these places. This can be done in
m+1Cn×1=m+1Cn ways.
Hence, the required number of ways m+1Cn
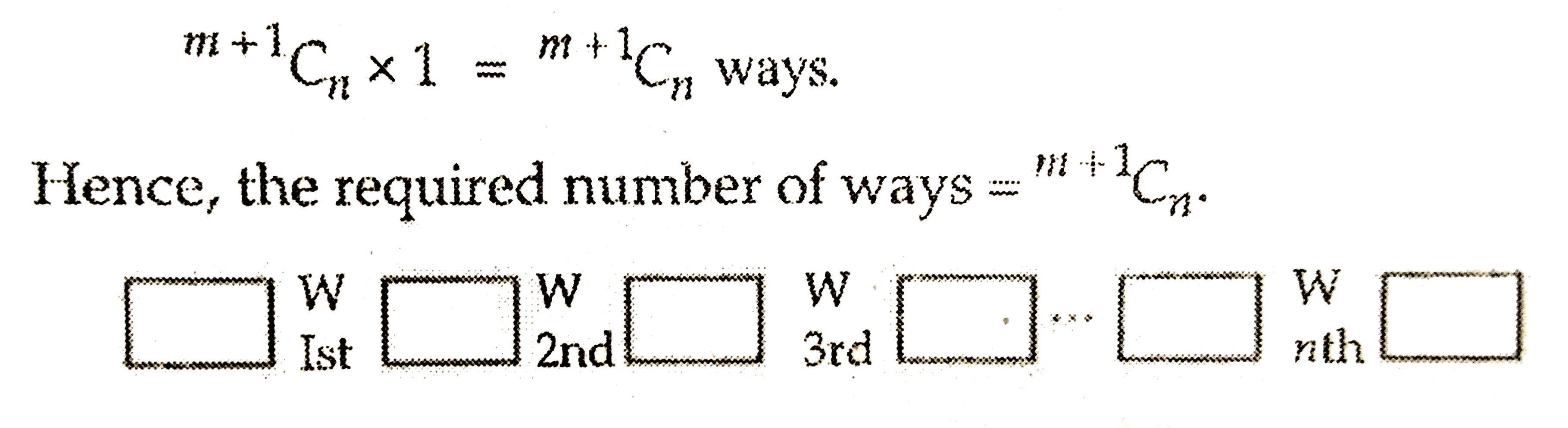
Topper's Solved these Questions
- BOOK - OBJECTIVE RD SHARMACHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Section I - Solved Mcqs111videos
PERMUTATIONS AND COMBINATIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Section II - Assertion Reason Type9videos
PERMUTATIONS AND COMBINATIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - PARABOLAEXERCISE - Chapter Test30videos
PARABOLA
- BOOK - OBJECTIVE RD SHARMACHAPTER - PROBABILITY EXERCISE - Chapter Test45videos
PROBABILITY
Similar Questions
Knowledge Check
- Question 1 - Select One
The number of ways of arranging m+ive signs n -ive signs (n<m+1) in a row so that no two -ive signs are together is
Am+1PnBm+1CnCn+1PmDn+1Cm - Question 2 - Select One
In how many ways can 21 identical white balls and 19 identical black balls be arranged in a row so that no 2 black balls are together?
A1540B1640C1240D1440
In how many ways can 7 red and 6 black balls be arranged in a row, if no two black balls are together?
View SolutionSeven white and 3 black balls are placed in a row. What is the probability if two black balls do not occur together ?
View SolutionFind the number of ways in which m boys and n boys and n girls may be arranged in a row so that no two of the girls are together, it being given that m>n.
View SolutionThe number of ways in which 5 Boys and 5 Girls can be arranged in a row so that no two girls are together is
View SolutionIf m is the number of ways in which six women and six men can be arranged to sit in row so that no two women are together and if n is the nnumber of ways they are seated in the same manner along a circle, then mn = _____________
View SolutionFind the number of ways in which 5 boys and 3 girls can be arranged in a row so that no two girls are together.
View Solution

