The number of ways in which 10 candidates A1,A2,A10 can be ranked such that A1 is always above A10 is a. 5! b. 2(5!) c. 10! d. 12(10!)
5!
2(5!)
10!
none of these
The correct Answer is:D
Step by step video, text & image solution for The number of ways in which 10 candidates A_1,A_2, A_(10) can be ranked such that A_1 is always above A_(10) is a. 5! b. 2(5!) c. 10 ! d. 1/2(10 !) by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - OBJECTIVE RD SHARMACHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Chapter Test60videos
PERMUTATIONS AND COMBINATIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Section II - Assertion Reason Type9videos
PERMUTATIONS AND COMBINATIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - PARABOLAEXERCISE - Chapter Test30videos
PARABOLA
- BOOK - OBJECTIVE RD SHARMACHAPTER - PROBABILITY EXERCISE - Chapter Test45videos
PROBABILITY
Similar Questions
Knowledge Check
- Question 1 - Select One
The number of ways in which ten candidates A1,A2,....,A10 can be ranked so that A1 is always above A2 is
A10!2B10!C9!D8!2 - Question 2 - Select One
The number of ways in which 10 condidates A1,A2,......,A10 can be ranked so that A1 is always above A2, is
A10!B10!2C9!Dnone of these - Question 3 - Select One
The capacitance of the capacitors of plate areas A1 and A2(A1<A2) at a distance d is
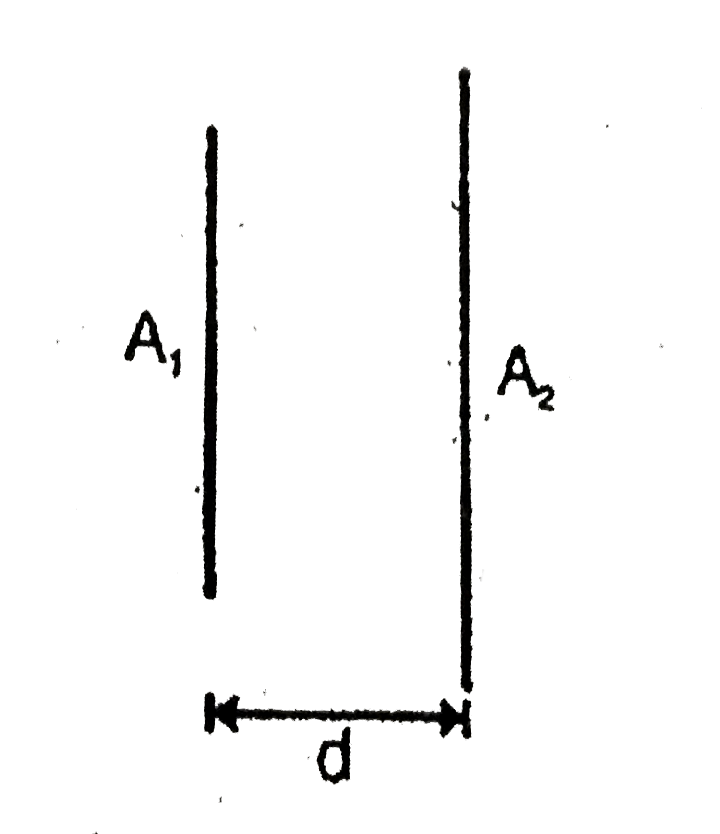 Aε0A1dBε0A2dCε0(A1+A2)2dDε0√A1A2d
Aε0A1dBε0A2dCε0(A1+A2)2dDε0√A1A2d
Find the number of ways of seating 10 students A1,A2.....A10 in a way that A1,A2,A3 sit together
View SolutionIn how many ways 10 persons A1,A2,A3,A4,...,.,A10 can be seated along a row such that A2,A3,A4 sit always after A1 is..
View SolutionIn how many 10 persons A1,A2,A3,.....A10 can be arranged along row in such a way that A2 must always occupy the middle place to that of A1,A3. (i) 20⋅8! (ii) 20⋅7! (iii) 40⋅7! (iv) 2!
View SolutionIf the points (a,b),(a1,b10and(a−a1,b−b1) are collinear, show that aa1=bb1
View SolutionIf 1,a1,a2,a3,…,an−1 are the nth roots of unity then prove that : 1+a1+a2+…+an−1=0.
View Solution

