Doubtnut Promotions Sticky

Let A={x−1≤x≤1}andf:A→A such that f(x)=x|x| then f is:

A

injective but not surjective

B

surjective but not injective

C

bijective

D

None of these

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:C

We have
f(x)=x|x|{x2x≥0−x2x<0
The graph, f(x) is shown in Fig. 10
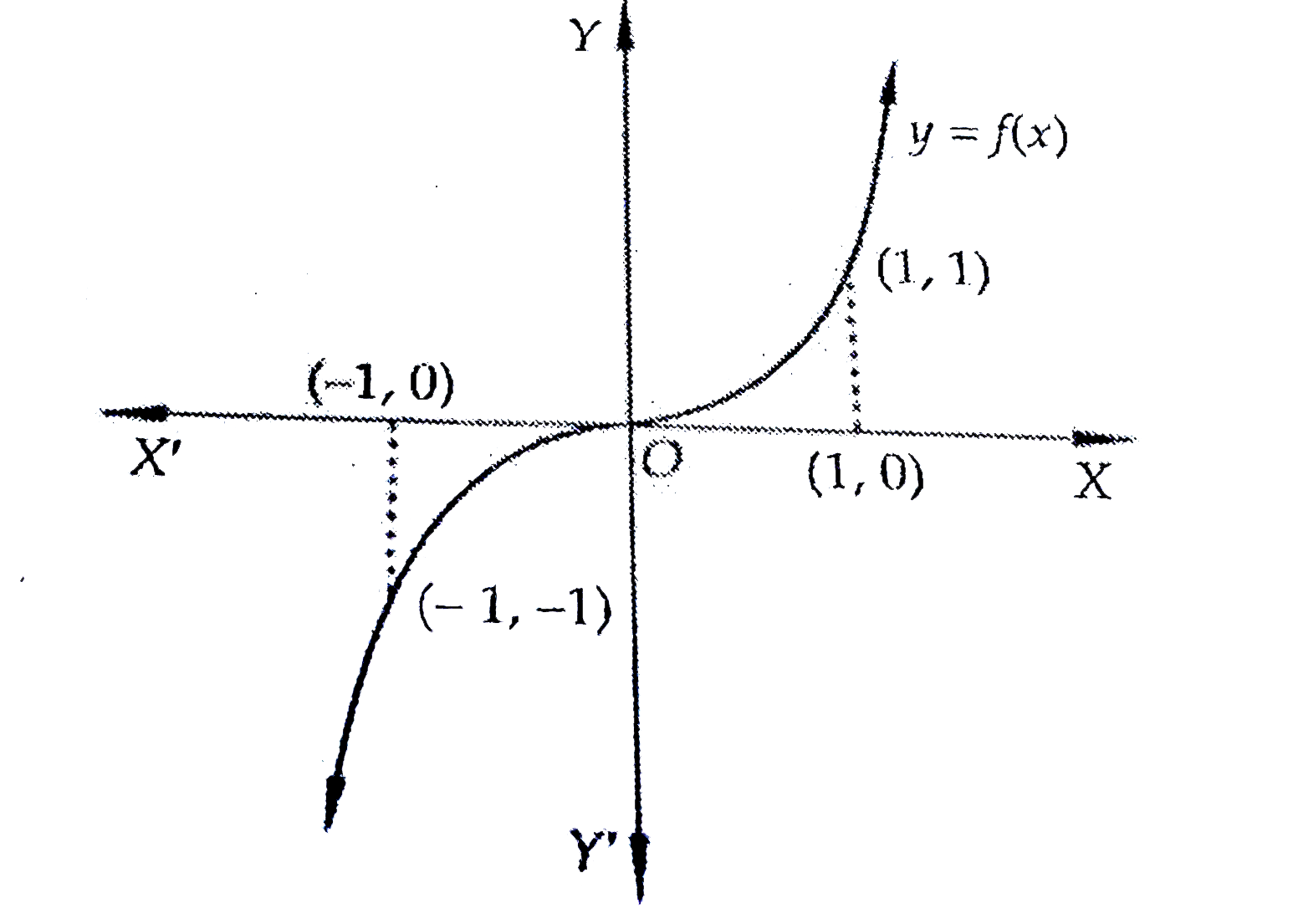
ocr_image
Clearly, f is a bijective

|
Updated on:21/07/2023
Class 11MATHSRELATIONS AND FUNCTIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    Let A={−1≤x≤1}andf:A→A such that f(x)=x|x| then f is:

    Aa bijection
    Binjective but not surjective
    Csurjective but not injective
    Dneither injective nor surjective
  • Question 2 - Select One

    Let f(x)={−1−2≤x<0x2−10≤x≤2 and g(x)=|f(x)|+f(|x|). Then , in the interval (-2,2),g is

    Anot differentiable at one point
    Bnot differentiable at two points
    Cdifferentiable at all points
    Dnot continuous
  • Question 3 - Select One

    Let f(x) be defined by
    f(x)={sin2xif 0<x≤π/6ax+bif π/6<x≤1
    The values of a and b such that f and f' are continuous, are

    Aa=1,b=1/√2+π/6
    Ba=1/√2,b=1/√2
    Ca=1,b=√3/2−π/6
    Dnone of these