The value of (30C0)(3010)−(301)(3011)+(302)(3012)++(3020)(3030)= ^60C20 b. ^30C10 c. ^60C30 d. ^40C30
A
30C11
B
60C10
C
30C10
D
65C55
Video Solution
Text Solution
The correct Answer is:c
We have,
30C0×30C10−30C1×30C11+...+30C10×30C0
= Coefficient of x20 in {(1+x)30(1−x)30}
= Coefficient of x20 in (1−x2)30
=30C10(−1)10=30C10
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - OBJECTIVE RD SHARMACHAPTER - BINOMIAL THEOREM AND ITS APPLCIATIONS EXERCISE - Section I - Assertion Reason Type13videos
BINOMIAL THEOREM AND ITS APPLCIATIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - BINOMIAL THEOREM AND ITS APPLCIATIONS EXERCISE - Exercise107videos
BINOMIAL THEOREM AND ITS APPLCIATIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - BINOMIAL THEOREM AND ITS APPLCIATIONS EXERCISE - Chapter Test60videos
BINOMIAL THEOREM AND ITS APPLCIATIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - CARTESIAN CO-ORDINATE SYSTEM EXERCISE - Exercise29videos
CARTESIAN CO-ORDINATE SYSTEM
Similar Questions
Knowledge Check
- Question 1 - Select One
The value of tan30∘+tan60∘cos30∘ is:
tan30∘+tan60∘cos30∘ का मान है :A√3+3B8/3C8/√3D1+√3 - Question 2 - Select One
The value of (300)(3010)−(301)(3011)+(302)(3012)++(3020)(3030)= ^60C20 b. ^30C10 c. ^60C30 d. ^40C30
A40C20B30C10C60C30D40C30 - Question 3 - Select One
The value of10∑r=0(−1)r.410−r30Cr30−rC10−r is equal to
A.30C10×210B.30C9×410C.30C10×310D.30C9×410
The value of (30,0)(30,10)−(30,1)(30,11)+(30,2)(30,11)−.............+(30,20)(30,30), where (n,r)=nCr is a. (30,10) b. (30,15) c. (60,30) d. (31,10)
View SolutionIn Figure, the value of x is (a) 12 (b) 15 (c) 20 (d) 30
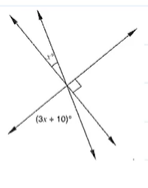 View Solution
View SolutionIn Figure, the value of y is 200 (b) 300 (c) 450 (d) 600
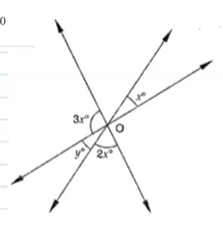 View Solution
View SolutionThe value cos30∘.cos60∘−sin30∘.sin60∘ is:
View SolutionWhat is the value of sin30∘+cos30∘cos30∘−sin30∘
View Solution

