Doubtnut Promotions Sticky

If ¯¯¯E and ¯¯¯F are the complementary events of E and F respectively and if 0<P(F)<1, then

A

P(E/F)+P(¯¯¯E/F)=1

B

P(E/F)+P(E/¯¯¯F)=1

C

P(¯¯¯E/F)+P(E/¯¯¯F)=1

D

P(E/¯¯¯F)+P(¯¯¯E/¯¯¯F)=1

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A, D

Since E/F and ¯¯¯E/F are complementary events.
∴P(E/F)+P(¯¯¯E/F)=1
Similarly, E/¯¯¯F and ¯¯¯E/¯¯¯F are also complementary events.
∴P(E/¯¯¯F)+P(¯¯¯E/¯¯¯F)=1

|
Updated on:21/07/2023
Class 11MATHSPROBABILITY

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

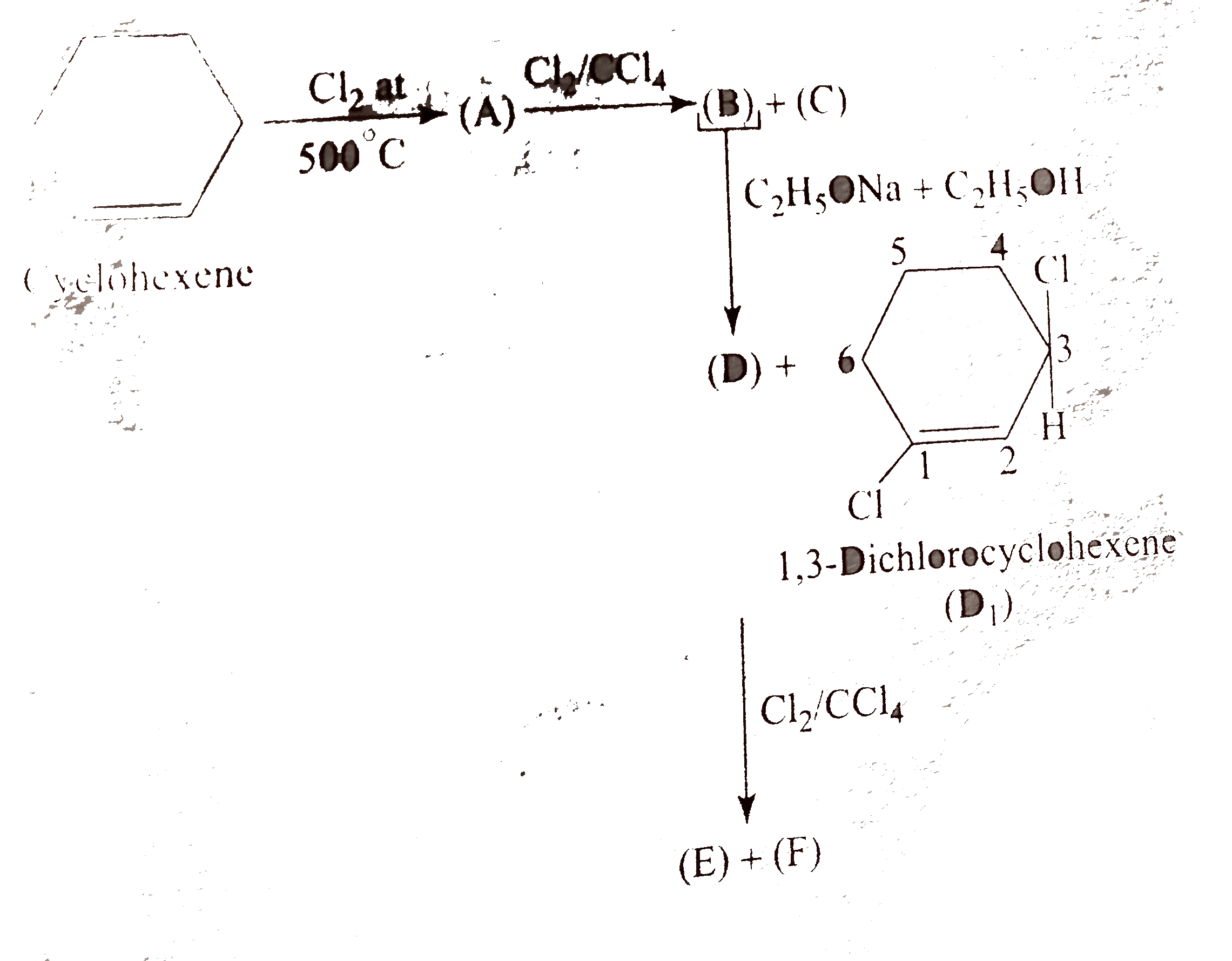
    ocr_image
    (E) and (F), respectively, are :

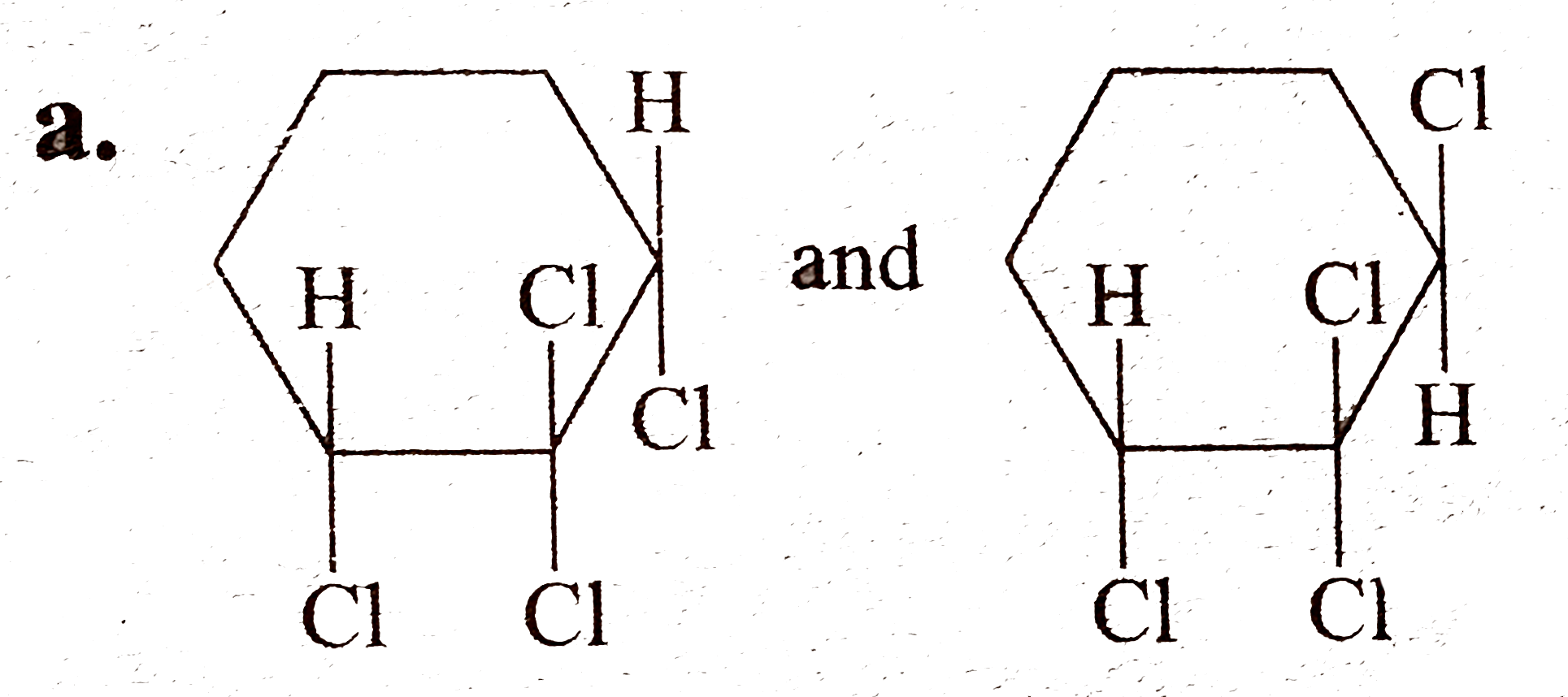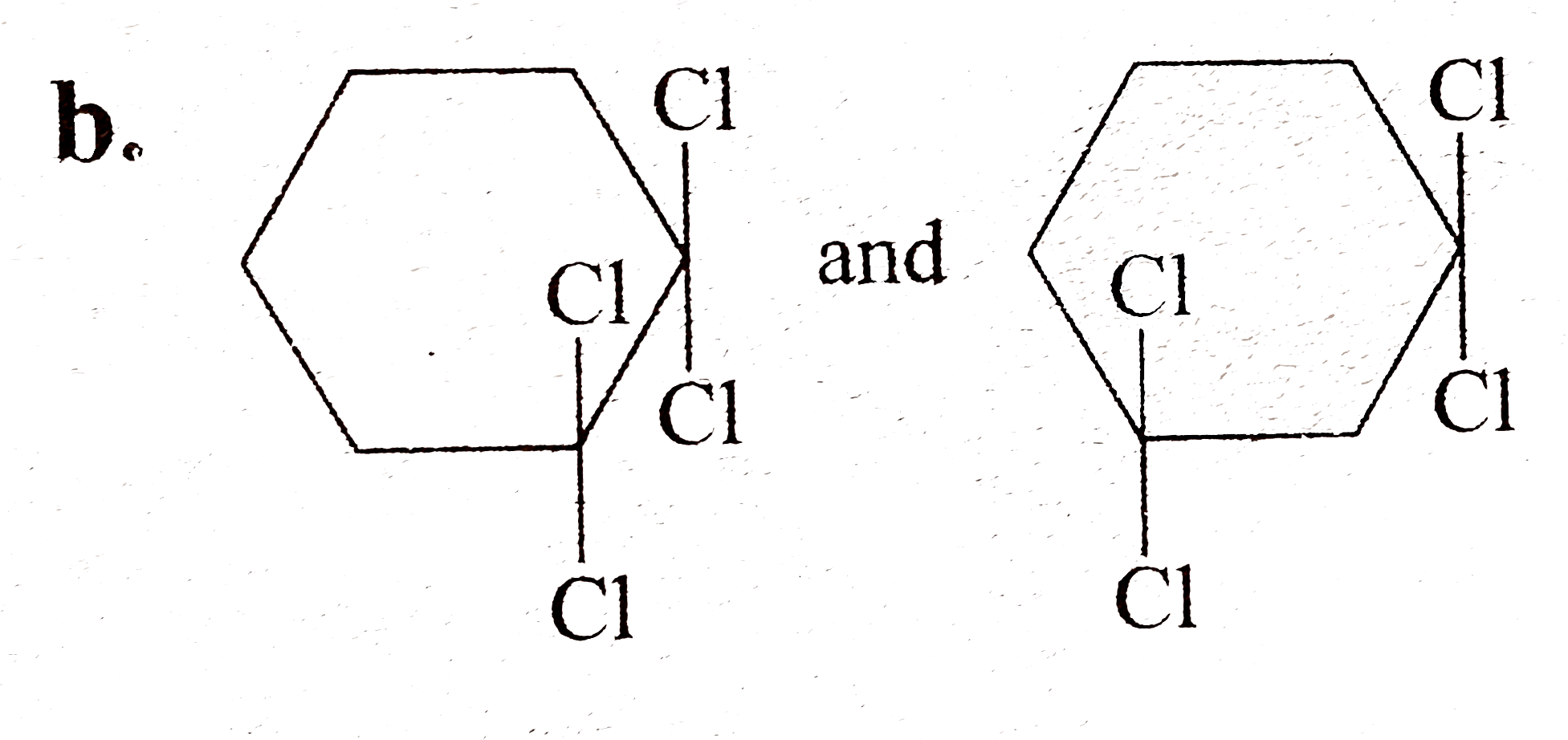    Aocr_image
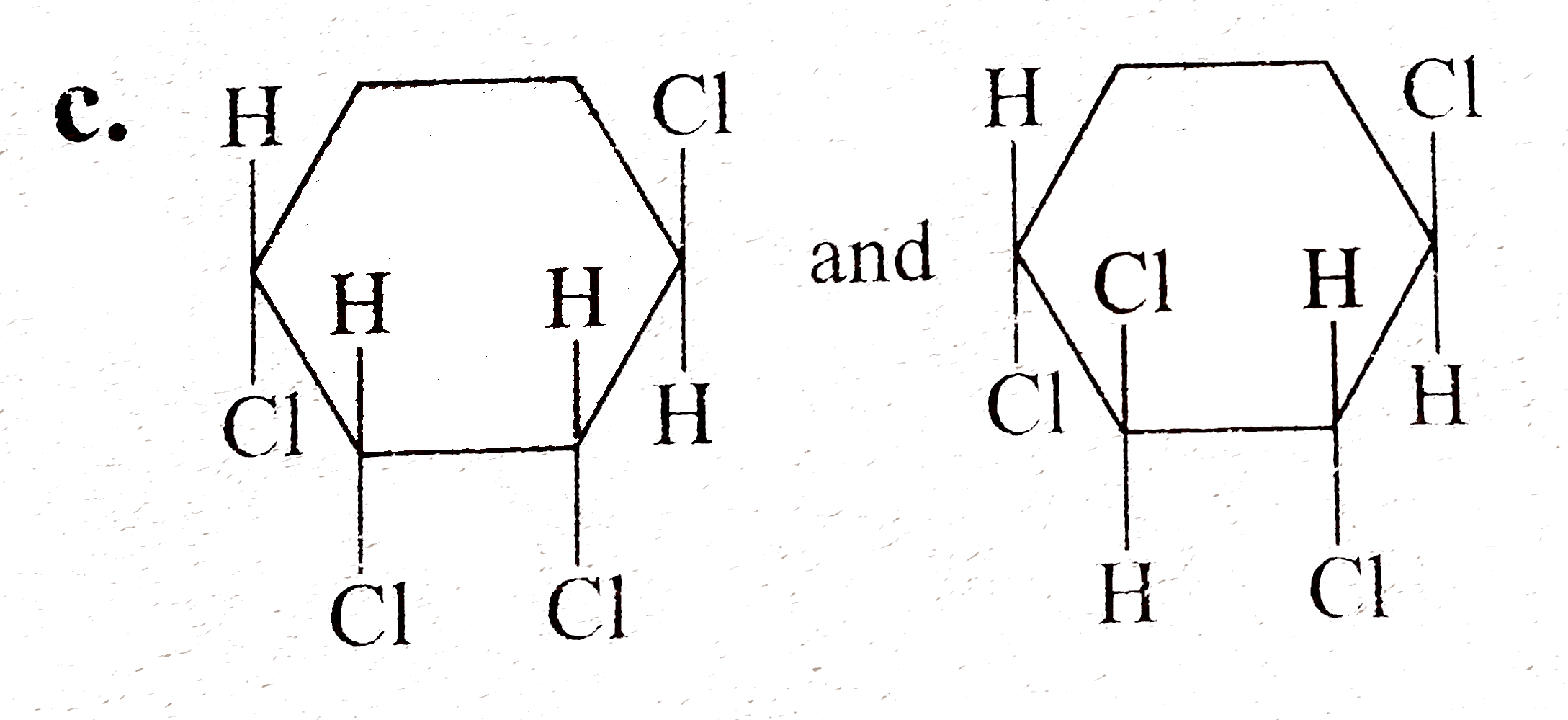    Bocr_image
    Cocr_image
    Docr_image
  • Question 2 - Select One

    If F0 andFe are the focal lengths of the objective and eye-piece respectively for a Galilean telescope, its magnifying power is about

    AF0+Fe
    BF0×Fe
    CF0/Fe
    D12F0+Fe
  • Question 3 - Select One

    If A',B' are complementary events of two independent events A, B, then P(A∪B)=

    A1−P(A)P(B')
    B1−P(A')P(B)
    C1−P(A')P(B')
    DP(A')+P(B')