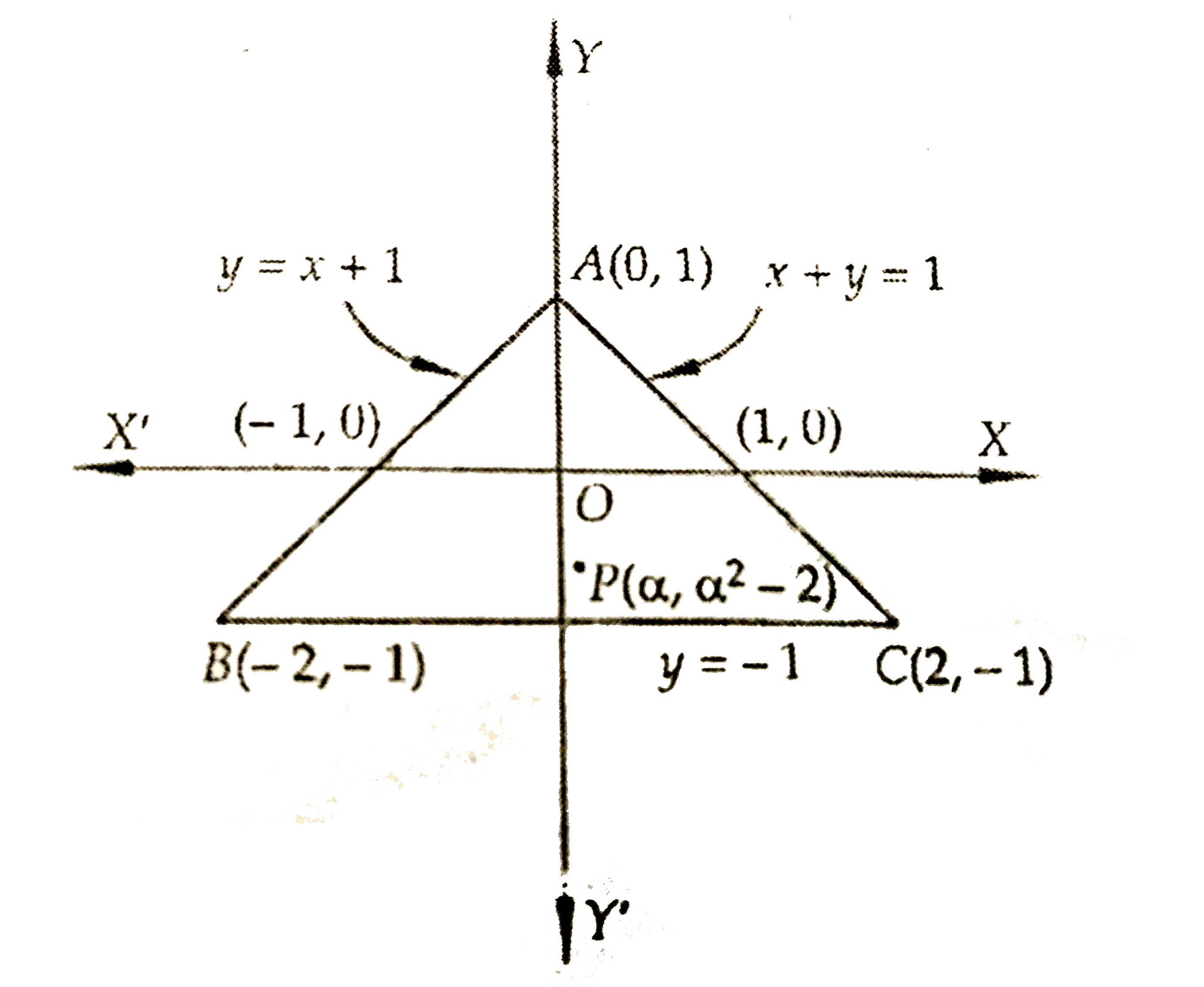
If point $P (α, α^{2} - 2)$ lies inside the triangle formed by the lines $x + y = 1, y = x + 1 and y = - 1$ then $α \in$

A

$(- \sqrt{3}, \sqrt{3})$

B

$(\frac{1 - \sqrt{13}}{2}, - 1) \cup (1, \frac{- 1 + \sqrt{13}}{2})$

C

[-1,1]

D

$(\frac{1 - \sqrt{13}}{2}, \frac{- 1 + \sqrt{13}}{2})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

(b) If point P $(α, α^{2} - 2)$ lies inside the $Δ$ ABC , then
(i) A and P must lie on the same side of BC whose equation is
$y + 1 = 0$
$∴ (1 + 1) (α^{2} - 2 + 1) > 0$
$\Rightarrow α^{2} - 1 > 0 \Rightarrow α \in (- \infty, - 1) \cup (1, \infty) ... (i)$
(ii) B and P must lie on the same side of AC .
$∴ (- 2 - 1 - 1) (α + α^{2} - 2 - 1) > 0$
$\Rightarrow α^{2} + α - 3 < 0 \Rightarrow \frac{- 1 - \sqrt{13}}{2} < α < \frac{- 1 + \sqrt{13}}{2} ... (i i)$

C and P must lie on the same side of AB .
$∴ (2 + 1 + 1) (α - α^{2} + 2 + 1) > 0$
$\Rightarrow α^{2} - α - 3 < 0 \Rightarrow \frac{1 - \sqrt{13}}{2} < α < \frac{1 + \sqrt{13}}{2} ... (i i i)$
From (i) and (ii) and (iii) , we have
$α \in (\frac{1 - \sqrt{13}}{2}, - 1) \cup (1, \frac{- 1 + \sqrt{13}}{2})$

|

Updated on:21/07/2023

Class 11 MATHS STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The complete set of values of the parameter $α$ so that the point $P (α, {(1 + α^{2})}^{- 1})$ does not lie outside the triangle formed by the lines $L_{1} : 15 y = x + 1, L_{2} : 78 y = 118 - 23 x$ and $L_{3} : y + 2 = 0$ is
A $(0, 5)$
B $[2, 5]$
C $[1, 5]$
D $[0, 2]$

OBJECTIVE RD SHARMA-STRAIGHT LINES-Section I - Solved Mcqs

Home
Ask Doubt
Profile