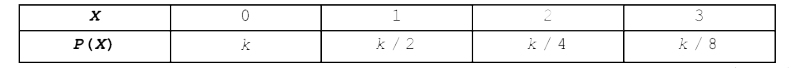If the probability of a random variable X is a given below :
X=x:−2−10123P(X=x):12k152k310k
Then the value of k, is :
110
210
310
710
The correct Answer is:A
To find the value of k in the given probability distribution, we need to ensure that the total probability sums to 1. The probabilities associated with the random variable X are given as follows:
X:−2,−1,0,1,2,3P(X=x):12,k,15,2k,310,k
Step 1: Write the equation for total probability
The total probability must equal 1. Therefore, we can write the equation as:
P(X=−2)+P(X=−1)+P(X=0)+P(X=1)+P(X=2)+P(X=3)=1
Substituting the values, we get:
12+k+15+2k+310+k=1
Step 2: Combine like terms
Now, we combine the terms involving k and the constant terms:
12+15+310+(k+2k+k)=1
This simplifies to:
12+15+310+4k=1
Step 3: Convert fractions to a common denominator
To combine the fractions, we can convert them to have a common denominator. The least common multiple of 2, 5, and 10 is 10. Thus, we convert:
12=510,15=210,310=310
Now substituting back, we have:
510+210+310+4k=1
Step 4: Combine the fractions
Now combine the fractions:
5+2+310+4k=1
This simplifies to:
1010+4k=1
Step 5: Solve for k
Since 1010=1, we can rewrite the equation as:
1+4k=1
Subtracting 1 from both sides gives:
4k=0
Dividing by 4, we find:
k=0
Step 6: Verify the solution
To ensure that this value of k is correct, substitute k=0 back into the probabilities:
P(X=−2)=12,P(X=−1)=0,P(X=0)=15,P(X=1)=0,P(X=2)=310,P(X=3)=0
Calculating the total probability:
12+0+15+0+310+0=510+210+310=1010=1
Thus, the total probability is indeed 1.
Final Answer
The value of k is:
0
The total probability must equal 1. Therefore, we can write the equation as:
Now, we combine the terms involving k and the constant terms:
To combine the fractions, we can convert them to have a common denominator. The least common multiple of 2, 5, and 10 is 10. Thus, we convert:
Now combine the fractions:
Since 1010=1, we can rewrite the equation as:
To ensure that this value of k is correct, substitute k=0 back into the probabilities:
The value of k is:
Topper's Solved these Questions
- DISCRETE PROBABILITY DISTRIBUTIONSBOOK - OBJECTIVE RD SHARMACHAPTER - DISCRETE PROBABILITY DISTRIBUTIONSEXERCISE - Section I - Solved Mcqs
39 Videos
- DISCRETE PROBABILITY DISTRIBUTIONSBOOK - OBJECTIVE RD SHARMACHAPTER - DISCRETE PROBABILITY DISTRIBUTIONSEXERCISE - Section II - Assertion Reason Type
1 Videos
- DETERMINANTSBOOK - OBJECTIVE RD SHARMACHAPTER - DETERMINANTSEXERCISE - Chapter Test
30 Videos
- FUNCTIONSBOOK - OBJECTIVE RD SHARMACHAPTER - FUNCTIONSEXERCISE - Chapter Test
30 Videos
Similar Questions
Knowledge Check
If X is a random -variable with distribution given below :
x:0123p(x):k3k3kk
The value of k and its variance areA1/8,22/27B1/8,23/27C1/8,24/27D1/8,3/4The probability distribution of a discrete random variable X is given below

The value of k isA8B16C32D48The probability distribution of a random variable X is given as follows:

If E(X)=2.3 , then value of k isA1/2B5/4C3D2
The probability distribution of discrete random variable X is given below
x2345P(x)5K7k9k11k
find the value of K.
View SolutionA random variable X has the following probability distribution: [X=x0123P(X=x)181214k]
View SolutionThe probability distribution of a discrate random variable X is :
X=x12345P(X=x)k2k3k4k5k
Find P(X≤4).
View SolutionIf the probability distribution of a random variable X is given by X=xi: 1 2 3 4 P(X=xi): 2k 4k 3k k Write the value of k .
View SolutionThe probability distribution of a discrete random variable X is given below: X: 2 3 4 5 P(X):5k 7k 9k 11k The value of E(X) is a. 8 b. 16 c. 32 d. 48
View Solution