If the roots of the equation ax2+bx+c=0 are real and distinct, then
both roots are greater than −b2a
both roots are less than −b2a
one of the roots exceeds −b2a
none of these
The correct Answer is:C
The roots of the given equation are
α=−b−√b2−4ac2aandβ=−b+√b2−4ac2a
Since α,β are real and distinct, therefore b2−4ac>0.
It is evident from Fig. 1 that β<−b2a<α.
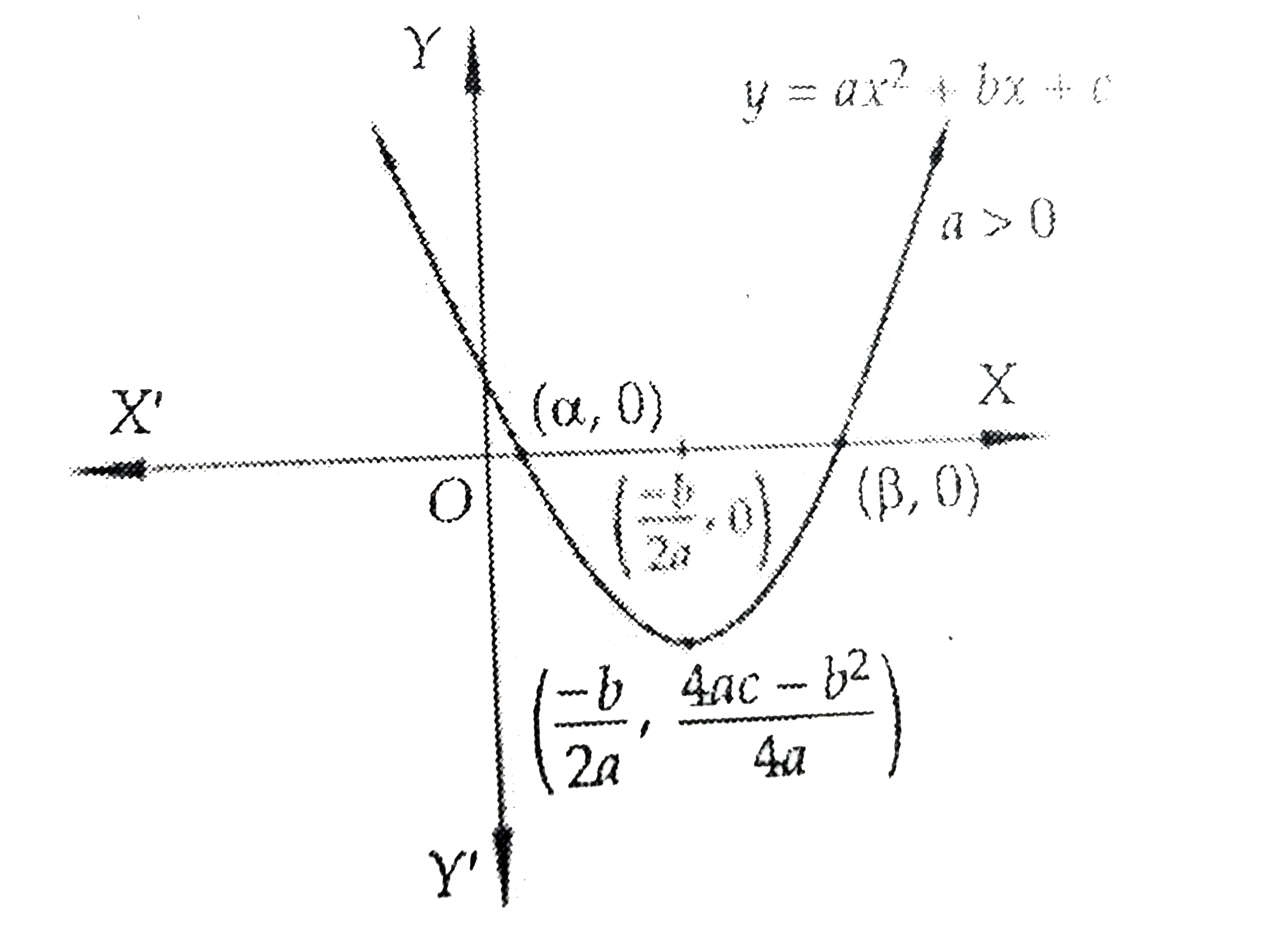
So, one root is less than −b2a and other exceeds −b2a.
Topper's Solved these Questions
- QUADRATIC EXPRESSIONS AND EQUATIONS BOOK - OBJECTIVE RD SHARMACHAPTER - QUADRATIC EXPRESSIONS AND EQUATIONS EXERCISE - Section I - Solved Mcqs
123 Videos
- QUADRATIC EXPRESSIONS AND EQUATIONS BOOK - OBJECTIVE RD SHARMACHAPTER - QUADRATIC EXPRESSIONS AND EQUATIONS EXERCISE - Section II - Assertion Reason Type
22 Videos
- PROBABILITY BOOK - OBJECTIVE RD SHARMACHAPTER - PROBABILITY EXERCISE - Chapter Test
45 Videos
- SEQUENCES AND SERIESBOOK - OBJECTIVE RD SHARMACHAPTER - SEQUENCES AND SERIESEXERCISE - Chapter Test
60 Videos
Similar Questions
If aandc are the lengths of segments of any focal chord of the parabola y2=bx,(b>0), then the roots of the equation ax2+bx+c=0 are real and distinct (b) real and equal imaginary (d) none of these
View SolutionIf all roots of the equation x3+ax2−ax−1=0 are real and distinct,then the set of values of a is
View Solution
Knowledge Check
If the roots of the equation ax2+bx+c=0 are equal then c=?
A−b2aBb2aC−b24aDb24aIf both the roots of the equation ax2+bx+c=0 are zero, then
Ab = c = 0Bb=0,c≠0Cb≠0,c=0Dnone of theseIf a, b, c are positive and a = 2b + 3c, then roots of the equation ax2+bx+c=0 are real for
A∣∣ac−11∣∣≥4√7B∣∣ca−11∣∣≥4√7C∣∣∣bc+4∣∣∣≥2√7D∣∣∣cb−4∣∣∣≥2√7
If roots of the quadratic equation bx2−2ax+a=0 are real and distinct then
View SolutionGiven the roots of equation ax2+bx+c are real and distinct then the graph will lie in which quadrant
View SolutionProve that the roots of the quadratic equation ax2−3bx−4a=0 are real and distinct for all real a and b, where a≠b.
View SolutionIf the roots of the equation ax2+bx+c=0 are in the ratio of 3:4,
View SolutionIf b2>4ac then roots of equation ax4+bx2+c=0 are all real and distinct if: (a)b<0,a<0,c>0(b)b<0,a>0,c>0(c)b>0,a>0,c>0(d)b>0,a<0,c<0
View Solution
