Let f(x) = [ n + p sin x], x∈(0,π),n∈Z, p a prime number and [x] = the greatest integer less than or equal to x. The number of points at which f(x) is not not differentiable is :
A
p
B
p-1
C
2p+1
D
2p-1
Video Solution
Text Solution
The correct Answer is:D
We know that the greatest integer function [x] is neither continuous nor differentiable at integer points. Therefore, f(x)=[n+p sin x] is discontinuous and non-differentiable at those points where n+psinx is an integer.
Clearly, n+p sin x will be an integer when p sin x is an integer Now, p sin x is an integer, if
sinx=1,1p,2p,3p,........,p−1p[∴x∈(0,π)∴sinx>0]
⇒x=sin−1(1),sin−1(2p),......sin−1(p−1p) at points
π−sin−11p,....mπ−sin−1(p−1p)also
Hence, the total number of points of discontiniuity of f(x) is (2p-1).
|
Topper's Solved these Questions
- CONTINUITY AND DIFFERENTIABILITYBOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Section II - Assertion Reason Type
13 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise
86 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise
86 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
59 Videos
- DEFINITE INTEGRALSBOOK - OBJECTIVE RD SHARMACHAPTER - DEFINITE INTEGRALSEXERCISE - Chapter Test 2
60 Videos
Similar Questions
Knowledge Check
Let |x| be the greatest integer less than or equal to x, Then f(x)=xcos(π(x+[x]) is continous at
Ax=−1Bx=0Cx=2Dx−1Let [x] denotes the greatest integer less than or equal to x. If f(x)=[xsinπx], then f(x) is
Acontinuous at x = 0Bcontinuous in (−1,0)Cdifferentiable at x = 1Ddifferentiable in (−1,1)Let [x] denotes the greatest integer less than or equal to x. If f(x)=[xsinπx], then f(x) is
Acontinuous at x=0,Bcontinuous in (-1,0),Cdifferentiable at x = 1Ddifferentiable in (-1,1),
If f(x)=|x−1|−[x] (where [x] is greatest integer less than or equal to x) then.
View SolutionIf f(x)=|x−1|−[x], where [x] is the greatest integer less than or equal to x, then
View SolutionLet f(x)=[cosx+sinx], 0<x<2π, where [x] denotes the greatest integer less than or equal to x. The number of points of discontinuity of f(x) is
View SolutionLet [x] denotes the greatest integer less than or equal to x. If f(x)=[xsinπx], then f(x) is
View SolutionLet [x] be the greatest integer less than or equal to x, for a real number x. Then the following sum
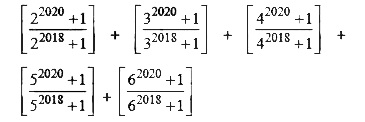
is-
View Solution
