Area bounded by $f (x) = \frac{(x - 1) (x + 1)}{x - 2}$ x-axis and ordinates $x = 0$ and $x = \frac{3}{2}$ is

A

$\frac{4}{5}$

B

$\frac{7}{8}$

C

1

D

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Clearly, f(x) is everwhere continuous and differentiable except at $x = 2 .$ The signs of f(x) for different values of x are shown in Fig. 11.

A rough sketch of the curve $y = f (x)$ is as shown in Fig. 12.

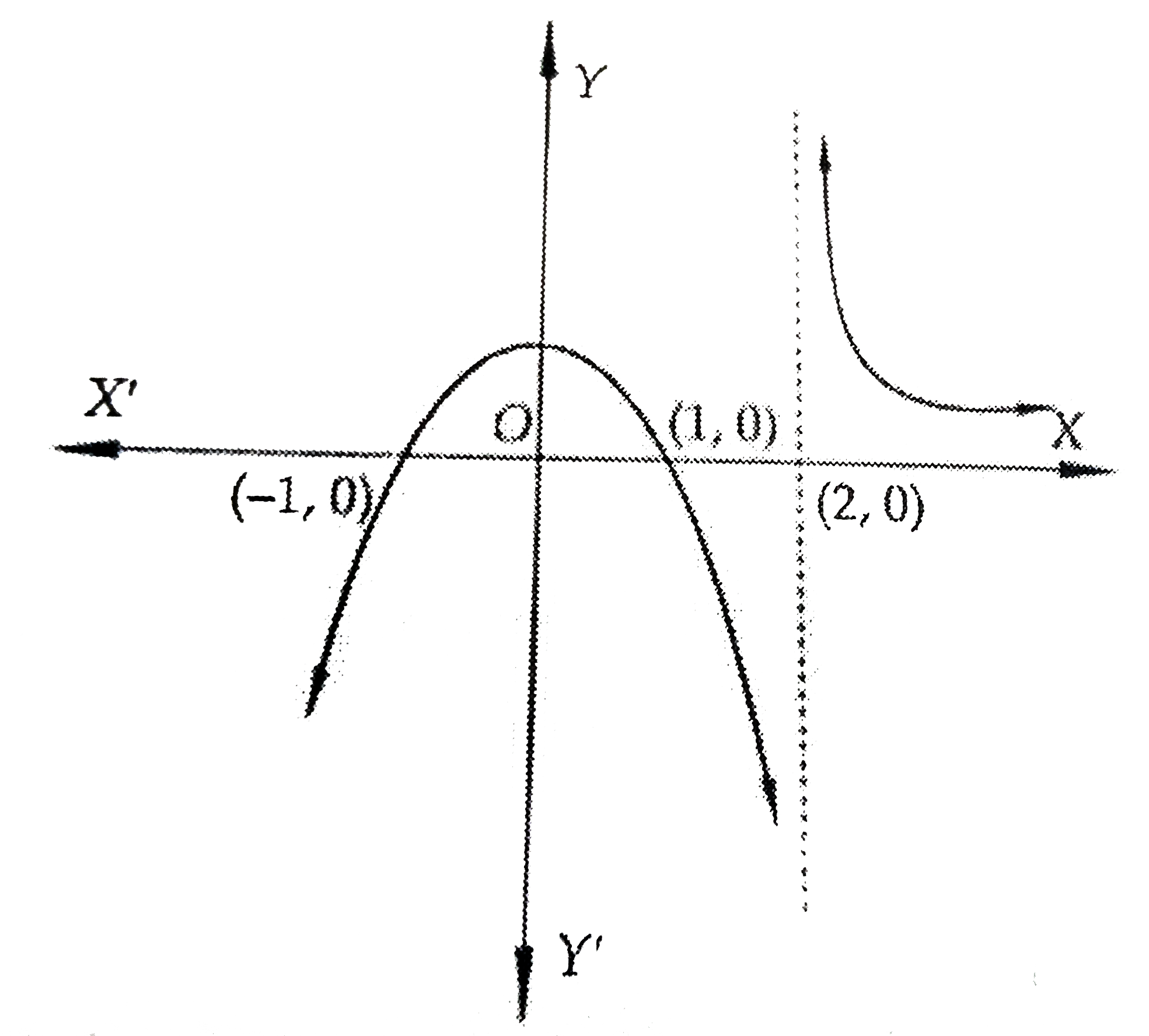
Let A denote the required area. Then,
$A = 3 / 2 \int 0 f (x) d x$
$\Rightarrow A = 1 \int 0 f (x) d x + ∣ ∣ ∣ ∣ ∣ 3 / 2 \int 1 f (x) d x ∣ ∣ ∣ ∣ ∣$
$\Rightarrow A = 1 \int 0 \frac{(x - 1) (x + 1)}{x - 2} d x - 3 / 2 \int 1 \frac{(x - 1) (x + 1)}{x - 2} d x$
$\Rightarrow A = 1 \int 0 (x + 2 + \frac{3}{x - 2}) d y - 3 / 2 \int 1 (x + 2 + \frac{3}{x - 2}) d x$
$\Rightarrow A = {[\frac{{(x + 2)}^{2}}{2} + 3 log | x - 2 |]}_{0}^{1} - {[\frac{{(x - 2)}^{2}}{2} + 3 log | x - 2 |]}_{1}^{3 / 2}$
$\Rightarrow A = (\frac{9}{2} - 2 - 3 log 2) = [(\frac{49}{8} + log \frac{1}{2}) - \frac{9}{2}] = \frac{7}{8}$ sq. units.

|

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

The area bounded by the curve $y = (x - 1) (x - 2) (x - 3)$ , x-axis and ordinates $x = 0, x = 3$ is :
A $\frac{9}{4}$
B $\frac{11}{4}$
C $\frac{11}{2}$
DNone of these
Area bounded by the curve $y = x^{2},$ the x-axis and the ordinates $x = - 2 and x = 1$ is :
A $- 9$
B $- \frac{15}{4}$
C $\frac{15}{4}$
D $\frac{17}{4}$
The area bounded by $y = 1 + \frac{8}{x^{2}}$ , X-axis and the ordinates x=2, x=4 is
A2
B4
Clog 2
Dlog 4

OBJECTIVE RD SHARMA-AREAS OF BOUNDED REGIONS-Chapter Test

Home
Ask Doubt
Profile