The area enclosed between the curves $y = x and y = 2 x - x^{2}$ (in square units), is

A

$\frac{1}{2}$

B

$\frac{1}{6}$

C

$\frac{1}{3}$

D

$\frac{1}{4}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Clearly,
Shaded Area $= 1 \int 0 {(2 x - x^{2}) - x} d x$
$\Rightarrow Shaded Area = 1 \int 0 (x - x^{2}) d x = {[\frac{x^{2}}{2} - \frac{x^{3}}{2}]}_{0}^{1} = \frac{1}{6}$

|

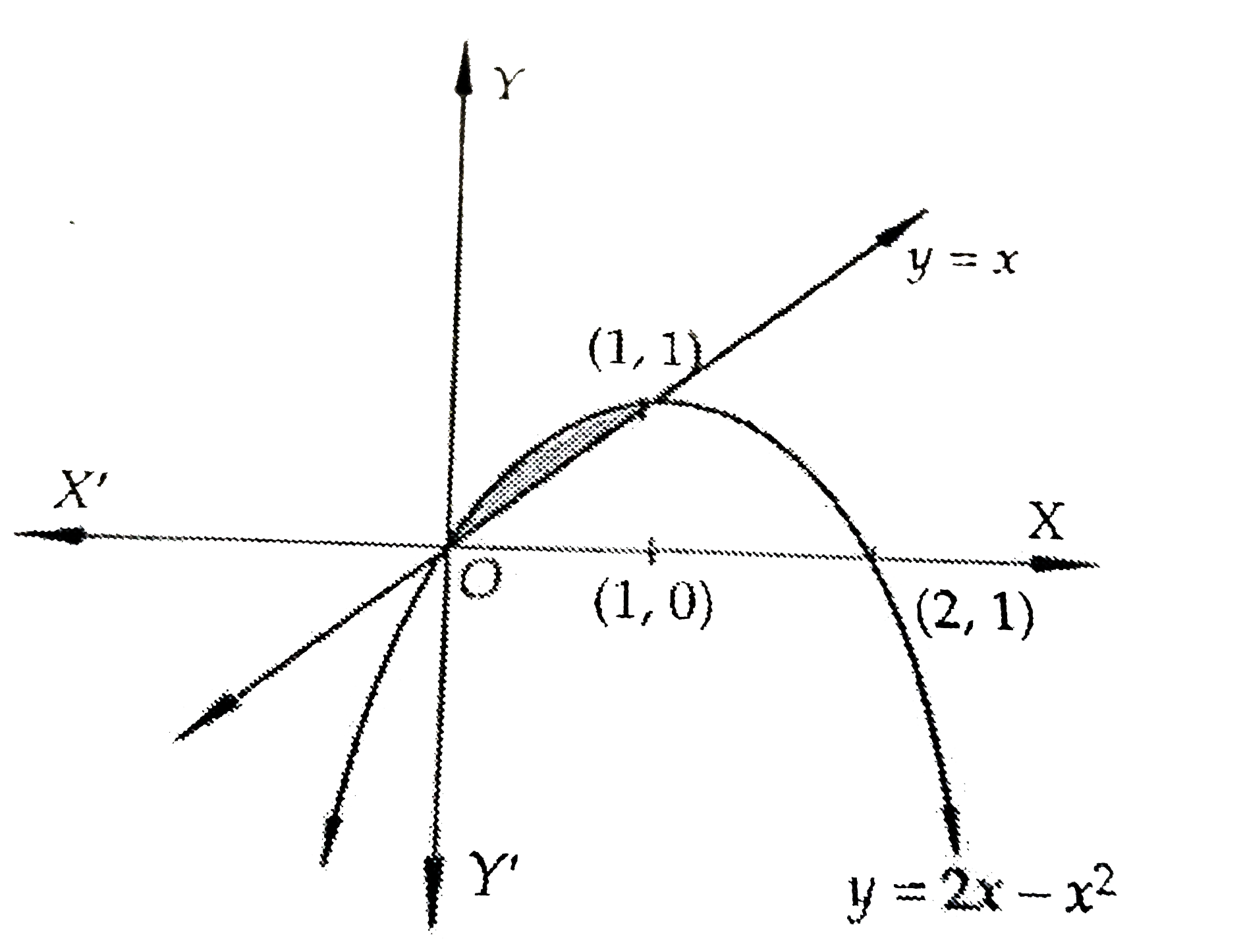
Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

BOOK - OBJECTIVE RD SHARMACHAPTER - AREAS OF BOUNDED REGIONSEXERCISE - Exercise
62videos
AREAS OF BOUNDED REGIONS
BOOK - OBJECTIVE RD SHARMACHAPTER - AREAS OF BOUNDED REGIONSEXERCISE - Chapter Test
60videos
AREAS OF BOUNDED REGIONS
BOOK - OBJECTIVE RD SHARMACHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Illustration
6videos
APPLICATION OF DERIVATIVES
BOOK - OBJECTIVE RD SHARMACHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test
31videos
CARTESIAN PRODUCT OF SETS AND RELATIONS

Similar Questions

Knowledge Check

Question 1 - Select One
The area enclosed between the curves $y^{2} = x and y = | x |$ is :
A $2 / 3$
B1
C $1 / 6$
D $1 / 3$
Question 2 - Select One
The area enclosed between the curves $y = x^{3}$ and $y = \sqrt{x}$ is
A $\frac{5}{3}$ sq units
B $\frac{5}{4}$ sq units
C $\frac{5}{12}$ sq unit
D $\frac{12}{5}$ sq units
Question 3 - Select One
The area enclosed between the curves $y = x^{3}$ and $y = \sqrt{x}$ is [in sq unit]
A44319
B44320
C44328
D44535

OBJECTIVE RD SHARMA-AREAS OF BOUNDED REGIONS-Chapter Test

Home
Ask Doubt
Profile