The area enclosed between the curve and the coordinate axes is
A
4
B
3
C
2
D
1
Video Solution
Text Solution
The correct Answer is:D
The area enclosed by and the coorcinate axes is shaded in Fig. 17.
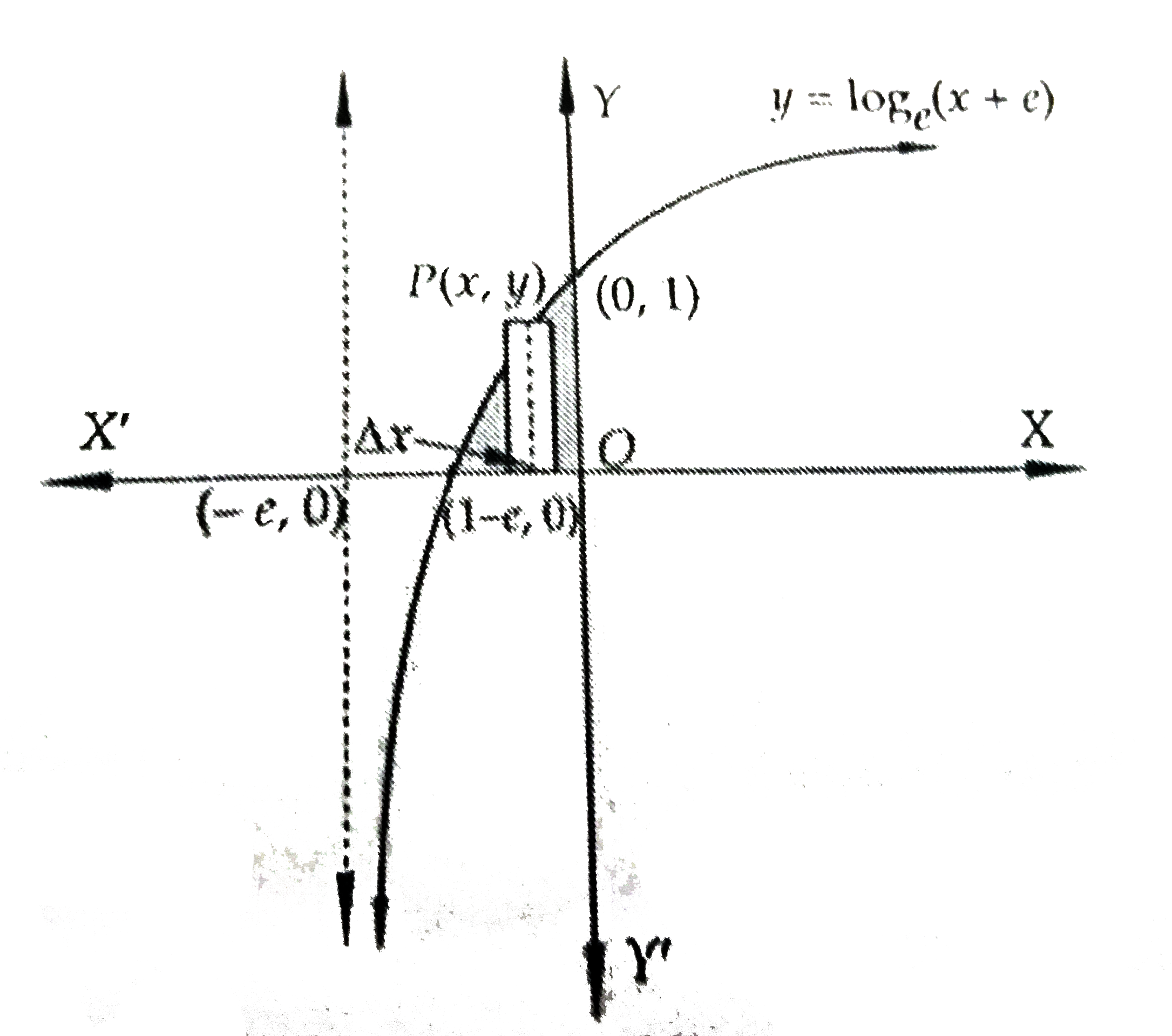
Let A be the required area. Then,
sq. units
|
Topper's Solved these Questions
- AREAS OF BOUNDED REGIONSBOOK - OBJECTIVE RD SHARMACHAPTER - AREAS OF BOUNDED REGIONSEXERCISE - Exercise
62 Videos
- AREAS OF BOUNDED REGIONSBOOK - OBJECTIVE RD SHARMACHAPTER - AREAS OF BOUNDED REGIONSEXERCISE - Chapter Test
60 Videos
- APPLICATION OF DERIVATIVESBOOK - OBJECTIVE RD SHARMACHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Illustration
6 Videos
- CARTESIAN PRODUCT OF SETS AND RELATIONS BOOK - OBJECTIVE RD SHARMACHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test
31 Videos
Similar Questions
Knowledge Check
The area enclosed between the curve y=loge(x+e) and the coordinate axes is
A3B4C1D2The area enclosed between the curves y=x3 and y=√x is
A53 sq unitsB54 sq unitsC512 sq unitD125 sq unitsArea enclosed between the curve y=x2 and the line y = x is
A18B16C32D17
Find the area enclosed between the curve y=cos2x,0≤x≤π2 and the co-ordinate axes.
View SolutionThe area enclosed between the curves y2=xandy=|x| is
View SolutionThe area enclosed between the curves y=∣∣x3∣∣ and x=y3 is
View SolutionThe area enclosed between the curves y=(log)e(x+e),x=(log)e(1y), and the x-axis is 2sq.units (b) 1sq.units 4sq.units (d) none of these
View SolutionThe area enclosed between the curves y2=xandy=|x| is :
View Solution
