If R1={(x,y)∣y=2x+7, where x∈R and −5≤x≤5} is a relation. Then find the domain and Range of R1.
34
12
13
14
The correct Answer is:b
Clearly,
R1=b∫0(1−x)2dxandR2=1∫0(1−x)2dx
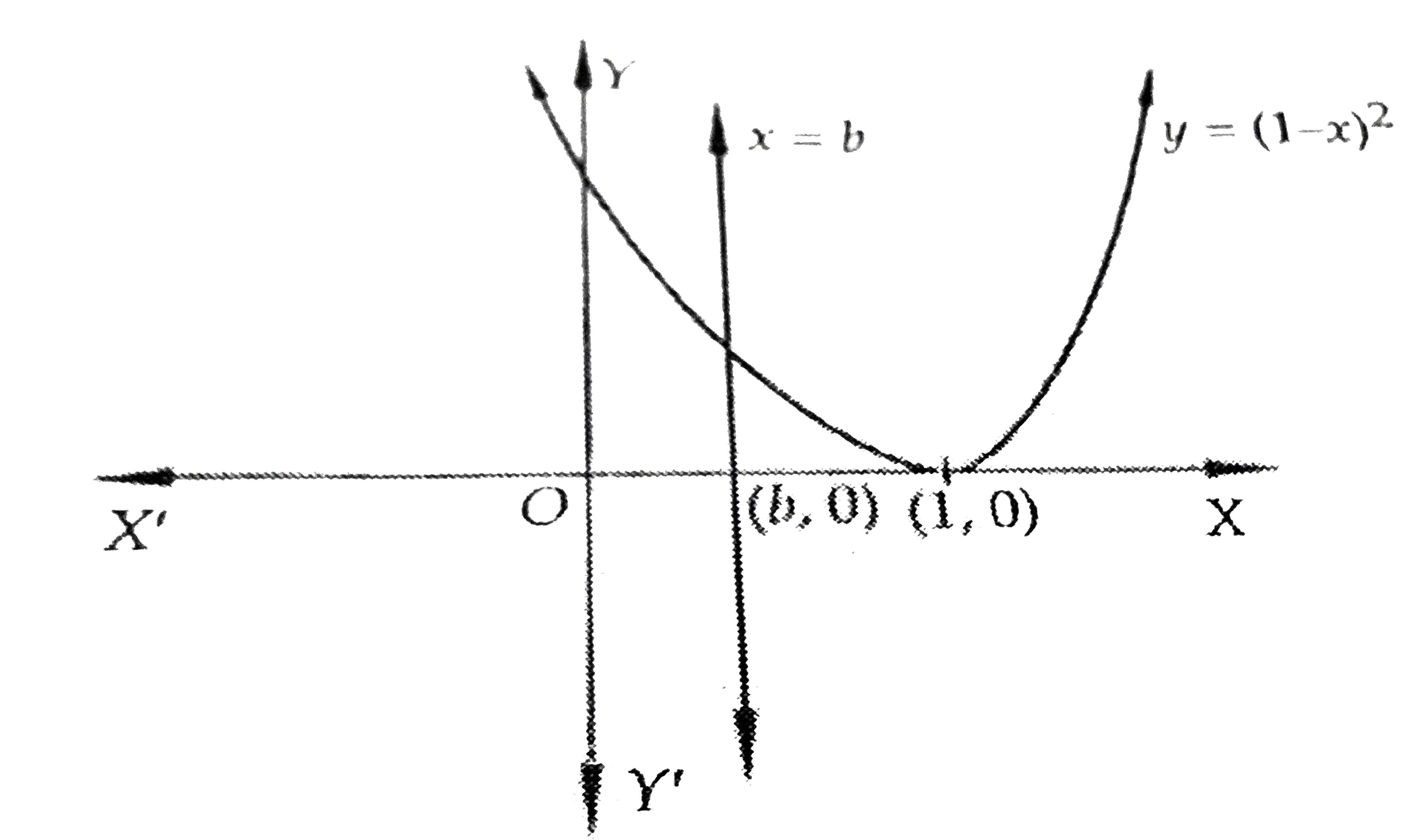
⇒R1=[(x−1)33]b0and,R2=[(x−1)33]1b
⇒R1=(b−1)33+13and,R2=−(b−1)33
∴R1−R2=14
⇒23(b−1)3+13=14
⇒23(b−1)3=−112
⇒(b−1)3=−18⇒b−1=−12⇒b=12
Topper's Solved these Questions
- AREAS OF BOUNDED REGIONSBOOK - OBJECTIVE RD SHARMACHAPTER - AREAS OF BOUNDED REGIONSEXERCISE - Exercise
62 Videos
- AREAS OF BOUNDED REGIONSBOOK - OBJECTIVE RD SHARMACHAPTER - AREAS OF BOUNDED REGIONSEXERCISE - Chapter Test
60 Videos
- APPLICATION OF DERIVATIVESBOOK - OBJECTIVE RD SHARMACHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Illustration
6 Videos
- CARTESIAN PRODUCT OF SETS AND RELATIONS BOOK - OBJECTIVE RD SHARMACHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test
31 Videos
Similar Questions
Knowledge Check
If R = {(x,y) : x,y ∈ Z , x2+y2≤4 } is a relation, then domain of R is
A{0,1,2}B{0,-1,-2}C{-2,-1,0,1,2}DNone of the above
If R={(x,y):x,y∈W,x2+y2=25}, then find the domain and range or R.
View SolutionIf A={1,2,3,4} and B={5,7,8,11,15}, are two sets and a relation R from A to B is defined as follows:
xRy⇔2x+3, where x∈A,y∈B
(i) Express R in Roaster form.
(ii) Find the domain and range of R.
(iii) Find R−1 .
(iv) Represent R by arrow diagram.
View SolutionIf R={(x,y):x,y∈W,2x+y=8} ., then write the domain and range of R.
View SolutionIf R={(x,y):x,y,∈Z,x2+3y2≤8} is a relation on the set of integers Z, then the domain R−1 is :
View SolutionLet A ={1,2,3,4,5,6,7,8} and R be the relation on A defined by :
R={(x,y):x∈A,y∈A and x+2y=10}.
Find the domains and ranges of R and R−1 after expressing them as sets of ordered pairs.
View SolutionA is a set of first 10 natural numbers and R is a relation from A to A defined as:
(x,y)∈R⇔x+2y=10 when x,y∈A
(i)Express R in the form of a set of ordered pairs.
(ii) Find the domain and range of R.
(iii) Find R−1 .
View SolutionLet A={1,2,3,4,5,6}. Define a relation R on set A by R={(x,y):y=x+1} Write down the domain, co domain and range of R.
View Solution
