For a curve (length of normal)(length of tangent) is equal to
A
subtangent
B
subnormal
C
slope of tangent
D
slope of normal
Video Solution
Text Solution
The correct Answer is:C
We have,
Length of normal =y√1+(dydx)2
Length of tangent=y√1+(dydx)2dydx
∴length of normallength of tangent=dydx= Slope of tangent
|
Topper's Solved these Questions
- TANGENTS AND NORMALSBOOK - OBJECTIVE RD SHARMACHAPTER - TANGENTS AND NORMALSEXERCISE - Section I - Solved Mcqs
49 Videos
- TANGENTS AND NORMALSBOOK - OBJECTIVE RD SHARMACHAPTER - TANGENTS AND NORMALSEXERCISE - Exercise
42 Videos
- SOLUTIONS OF TRIANGLES BOOK - OBJECTIVE RD SHARMACHAPTER - SOLUTIONS OF TRIANGLES EXERCISE - Exercise
20 Videos
- THREE DIMENSIONAL COORDINATE SYSTEM BOOK - OBJECTIVE RD SHARMACHAPTER - THREE DIMENSIONAL COORDINATE SYSTEM EXERCISE - Exercise
22 Videos
Similar Questions
Knowledge Check
IF two tangents inclined at an angle of 60∘ are drawn to a circle of radius 3 cm , then the length of each tangent is equal to
A3√32 cmB6 cmC3 cmD3√3cmIf two tangents inclined at an angle of 60∘ are drawn to a circle of radius 4 cm, then the length of each tangent is equal to :
A2√3 cmB8 cmC4 cmD4√3 cmThe differential equation of the family of curves for which the length of the normal is equal to a constant k, is given by
Ay2(dydx)2=k2−y2B[ydyDx]2=k2−y2Cydydx=k2−y2D[ydydx]2=k2+y2
If two tangents inlined at an angle 60∘ are drawn to a circle of radius 3 cm , then the length of each tangent is equal to :
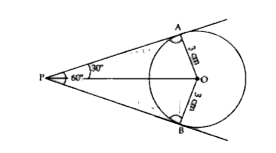
View SolutionIf two tangents inclined at an angle 60∘ are drawn to a circle of radius 3 cm, then, the length of each tangent is equal to
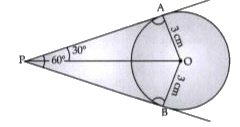
View SolutionA curve passes through (1,2) is such that the length of the normal at any of its point is equal to 2. The curve can be
View SolutionLength OF tangent || Power OF point
View SolutionThe curve for which the length of the normal is equal to the length of the radius vector is/are (a) circles (b) rectangular hyperbola (c) ellipses (d) straight lines
View Solution
