Let →u=u1ˆi+u2ˆj+u3ˆk be a unit vector in R3and→w=1√6(ˆi+ˆj+2ˆk) , Given that there exists a vector →v in R3 such that |→u×→v|=1and→w.(→u×→v)=1 which of the following statements is correct ?
There is exactly one choice for such →v
There are exactly two for such `vecv`
There are exactly for such →v
There are infinitely many choices for such →v
The correct Answer is:D
Clearly, →w is a unit vector such that |→u×→v|=1 and →w , (→u×→v)=1 Now, →w .(→u×→v) =1<br> ⇒→w = →u × →v
⇒|→w|=|→u×→v|
⇒1=|→u||→v|sinθ where θ is the angle betweeen →uand→v
⇒→csinθ=1
Clearly, p can take infinitely many positions on the line at a unit distance from OA. Consequently, −−→OP=→v has, infinitely, many chocies.
Topper's Solved these Questions
- SCALER AND VECTOR PRODUCTS OF TWO VECTORS BOOK - OBJECTIVE RD SHARMACHAPTER - SCALER AND VECTOR PRODUCTS OF TWO VECTORS EXERCISE - Section I - Solved Mcqs
12 Videos
- SCALAR AND VECTOR PRODUCTS OF THREE VECTORS BOOK - OBJECTIVE RD SHARMACHAPTER - SCALAR AND VECTOR PRODUCTS OF THREE VECTORS EXERCISE - Exercise
65 Videos
- SOLUTIONS OF TRIANGLES BOOK - OBJECTIVE RD SHARMACHAPTER - SOLUTIONS OF TRIANGLES EXERCISE - Exercise
20 Videos
Similar Questions
Knowledge Check
Let →u=u1ˆi+u2ˆj be a unit vector in xy plane and →w=1√6(ˆi+ˆj+2ˆk) . Given that there exists a vector →c " in " R3 " such that |→u×→v|=1 and →w. (→u×→v)=1 , then
A|u1|=|u2|B|u2|=2|u2|C2|u1|=|u2|D|u1|−3|u2|Let →u=u1ˆi+u3ˆk be a unit vector in xz-plane and →q=1√6(ˆi+ˆj+2ˆk). If there exists a vector →v in such that |→u×→u|=1and→w.(→u×→c) .Then
A|u1|=|u3|B|u1|=2|u3|C|u1|=2|u3|D2|u1|=|u3|Let →u=2ˆi−ˆj+ˆk,→v=−3ˆj+2ˆk be vectors in R3 and →w be a unit vector in the xy-plane. Then the maximum possible value of |(→u×→v).→w| is-
A√5B√12C√13D√17
The figure given below shows the orientation of two vectors →uand→v in the xy plane .
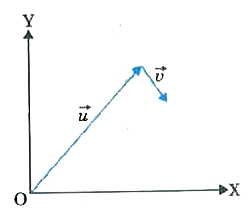
if →u=aˆi+bˆjand→v=pˆi+qˆj
Which of the following is correct ?
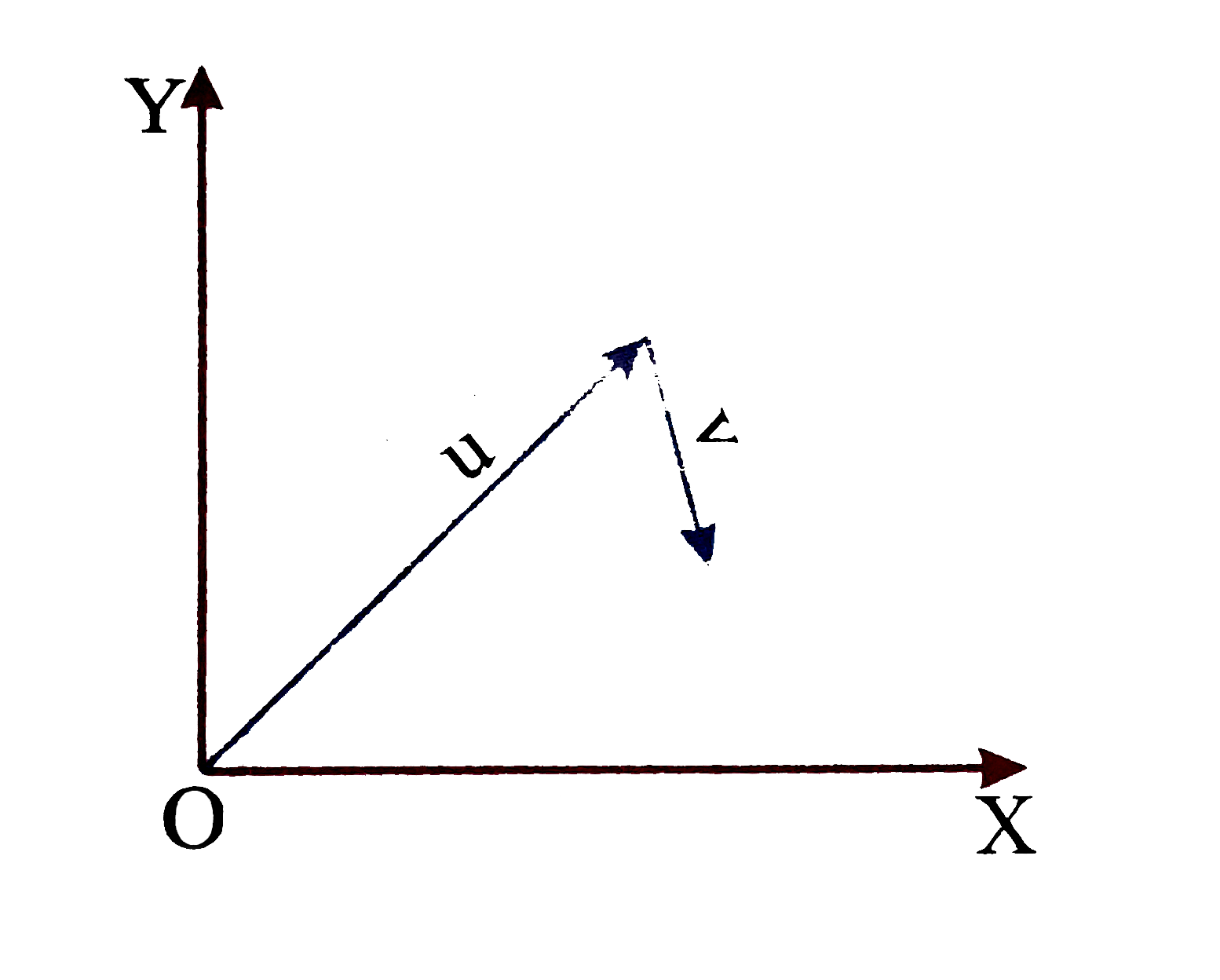
View SolutionFigure shows the orientation of two vectors u and vin the XY plane.
if→u=aˆi+bˆj and →v=pˆi+qˆj
which of the following is correct?
View SolutionThe unit vector parallel to the resultant vector of 2ˆi+4ˆj−5ˆkandˆi+2ˆj+3ˆk is
View SolutionFor three vectors, →u,→vand→w which of the following expressions is not equal to any of the remaining three ?
View SolutionLet →u=ˆi+ˆj,→v=ˆi−ˆjaandˆi−ˆjand→w=ˆi+2ˆj+3ˆk If ˆn isa unit vector such that →u.ˆn=0and→n.ˆn=0, then |→w.ˆn| is equal to
View Solution
