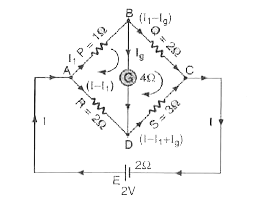
एक व्हीटस्टोन ब्रिज में P=1Ω,Q=2Ω,R=2Ω,S=3Ω और G=4Ω है। ब्रिज की असंतुलित अवस्था में गैल्वेनोमीटर में से बहने वाली धारा निकालें जब 2Ω आन्तरिक प्रतिरोध वाला 2 V का सेल प्रयुक्त किया जाए।
दिए गए प्रतिरोध और सेल वाला व्हीटस्टोन ब्रिज, चित्र 6 . 22 में दिखाया गया है।
मान लें कि सेल में से कुल धारा l बहती है। परिपथ में धारा का वितरण किरखोफ के पहले नियम के अनुसार दिखाया गया है। हमें ब्रिज की असंतुलित अवस्था में गैल्वेनोमीटर में से बहने वाली धारा lg निकालनी है। बन्द लूप ABDA पर किरखोफ का दूसरा नियम लगाते हुए हम प्राप्त करते हैं
l1×1+lg×4−(1−l1)×2=0
या 3l1−2l+4lg=0 . . . (i)
बन्द लूप BCDB पर किरखोफ का दूसरा नियम लगाते हुए हम प्राप्त करते हैं
2(l1−lg)−3(l−l1+lg)−4lg=0
या 5l1−3l−9lg=0 . . . (ii)
फिर बन्द लूप ADCEA पर किरखोफ का दूसरा नियम लगाते हुए हम प्राप्त करते हैं
2(l−lg+3(l−l1+lg)+2l=2
या −5l1+7l+3lg=2 . . . (iii)
समीकरण (ii) और (iii) को जोड़ने पर
4l−6lg=2 . . . (iv)
समीकरण (i) को 5 से और समीकरण (ii) को 3 से गुणा करने पर हम प्राप्त करते हैं
15l1−10l+20lg=0 . . . (v)
और 15l1−9l−27lg=0 . . . (iv)
समीकरण (v) में से समीकरण (vi) घटाते हुए
−l+47lg=0 या l=47lg
इस प्रकार समीकरण (iv) से
4×47lg−6lg=2
या 182lg=2 ,
lg=2182=0.011A या
Topper's Solved these Questions
- विद्युत परिपथ , विद्युत ऊर्जा और शक्ति BOOK - GRB PUBLICATION HINDICHAPTER - विद्युत परिपथ , विद्युत ऊर्जा और शक्ति EXERCISE - उच्चस्तरीय चिंतन : प्रश्नोत्तरी
9 Videos
- विद्युत परिपथ , विद्युत ऊर्जा और शक्ति BOOK - GRB PUBLICATION HINDICHAPTER - विद्युत परिपथ , विद्युत ऊर्जा और शक्ति EXERCISE - प्रश्नोत्तरी : 1 अंक
18 Videos
- विद्युत परिपथ , विद्युत ऊर्जा और शक्ति BOOK - GRB PUBLICATION HINDICHAPTER - विद्युत परिपथ , विद्युत ऊर्जा और शक्ति EXERCISE - प्रतियोगिता सामग्री ( रिक्त स्थान भरना )
15 Videos
- प्रत्यावर्ती धाराएँ BOOK - GRB PUBLICATION HINDICHAPTER - प्रत्यावर्ती धाराएँ EXERCISE - रिक्त स्थान भरना
15 Videos
- वैद्युत क्षेत्र और गाउस नियमBOOK - GRB PUBLICATION HINDICHAPTER - वैद्युत क्षेत्र और गाउस नियमEXERCISE - NCERT पाठ्यपुस्तक अभ्यास : उत्तरो सहित
29 Videos
Similar Questions
एक बाहरी स्त्रोत द्वारा आवेशन के दौरान एक समान्तर प्लेट संधारित्र लें, जिसकी प्रत्येक प्लेट का क्षेत्रफल A है।
(a) सिद्ध करें कि स्रोत से धनात्मक प्लेट तक (या ऋणात्मक प्लेट से स्त्रोत तक) बहने वाली चालन धारा ε0(dEdt)A के बराबर है, जहाँ E, प्लेटों के बीच वैद्युत क्षेत्र है।
(b) क्या इस स्थिति में किरखोफ का पहला नियम मान्य है? । यदि नहीं, तो क्या आप नियम के व्यापकीकरण का तरीका सुझा सकते हैं ताकि यह यहाँ भी मान्य हो?
View Solutionपोटेशियोमीटर की तार आम तौर पर किस धातु की बनाई जाती है और क्यों?
View Solutionएक H-परमाणु में एक इलेक्ट्रॉन नाभिक के इर्द-गिर्द 6.6×1015 rps लगाता है। तुल्य धारा ..............A है।
View Solutionएक शुद्ध प्रेरकत्व में क्षयित हुई औसत शक्ति.........।
View Solutionहवा में एक दूसरे से 30 cm दूर रने 2×10−7C और 3×10−7C आवेश वाले दो छोटे आवेशित गोलों के बीच बल ज्ञात करें।
View Solution(2 + omega + omega ^ (2)) ^ (3) + (1 + omega-omega ^ (2)) ^ (3) = (1-3 omega + omega ^ (2)) ^ (4) = 1
View Solutionयदि 1 का तीन घनमूल 1,ω,ω2 हो तो दिखलाइए कि
(2+ω+ω2)3+(1+ω−ω2)8−(1−3ω+ω2)4=1
View Solutionयदि ,ω,ω2 इकाई के घनमूल है तो सिद्ध कीजिए कि -
(i) (1−ω+ω2)+(1+ω−ω2)=4
(ii) (1+ω)3−(1+ω2)3=0
(iii) (1−ω+ω2)3=(1+ω−ω2)3=−8
(iv) (1−ω+ω2)5+(1+ω−ω2)5=32
(v) (2+5ω+2ω2)6=(2+2ω+5ω2)6=729
(vi) (1+ω)(1+ω2)(1+ω4)(1+ω8)=1
View Solutionयदि 1,ω तथा ω2 इकाई के घनमूल है तो सिद्ध कीजिए कि -
(i) ω(1+ω−ω2)=−2
(ii) (1+ω−ω2)(ω+ω2−1)(ω2+1−ω)=−8
(iii) ω4+2ω6+ω8=1
(iv) (3+3ω+5ω2)6−(2+6ω+2ω2)3=0
(v) (1+ω)(1+ω2)(1+ω4)(1+ω8)=1
View SolutionProve that p+qω+rω2r+pω+qω2=ω2
View Solutionयदि w इकाई का एक घनमूल हो तो सारणिक ∣∣ ∣ ∣∣1w4w8w4w81w81w4∣∣ ∣ ∣∣का मान है-
View Solutionयदि ω इकाई का एक घनमूल हो, तो सारणिक ∣∣ ∣ ∣∣1ω4ω8ω4ω81ω81ω4∣∣ ∣ ∣∣ का मान है-
View Solutionयदि ω इकाई का एक काल्पनिक घन मूल है, तो सारणिक ∣∣ ∣ ∣∣1+ωω2−ω1+ω2ω−ω2ω+ω2ω−ω2∣∣ ∣ ∣∣ का मान है-
View Solutionयदि ω इकाई का घनमूल है, तो (1+ω−ω2)2+(1−ω+ω2)2+1 का मान होगा
View Solutionव्यंजक 1.(2−ω)(2−ω2)+2.(3−ω)(3−ω2)+.......+(n−1)(n−ω)(n−ω2), जहाँ ω एक इकाई का काल्पनिक घनमूल है, का मान है।
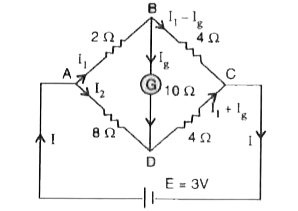
View SolutionDetermine the current through the galvanometer in the circuit. Given :P=2Ω,Q=4Ω,R=8ΩS=4ΩG=10Ω,E=5andr=0.
View Solution
