Here are examples of how to use Newton's second law for a quck when one or two forces act on it. Parts (a), (b), and ( c ) of Fig. 5-3 show three situations in which one or two forces act on a puck that moves over frictionless ice along an x axis, in one-dimensional motion. The puck's mass is m = 0.20 kg. Forces →F1 and →F2 are directed along the axis and have magnitudes F1=4.0 N and F2=2.0 N. Force →F3 is directed at angle θ=30∘ and has magnitude F3=1.0 N. In each situation, what is the acceleration of the puck ?
In each situation we can relate the acceleration →a to the net force →Fnet acting on the puck with Newton.s second law, →Fnet=m→a. However, because the motion is along only the x axis, we can simplify each situation by writing the second law for x components only:
Fnet.x=max. (5−4)
The free-body diagrams for the three situations are also given in Fig. 5-3, with thee puck represented by a dot.
Calculations :
Situation A: Foor Fig. 5-3b, where only one horizontal force acts, Eq. 5-4 gives us
F1=max,
which, with given data, yields
ax=F1m=4.0N0.20kg=20 m/s2.
The positive answer indicates that the acceleration is in the positive direction of the x axis.
Situation B: In Fig. 5-3d, two horizontal forces act on the puck, →F1 in the positive direction of x and →F2 in the negative direction. Now Eq. 5-4 gives us
F1−F2=max,
which, with given data, yields
ax=F1−F2m=4.0N−2.0N0.20kg=10 m/s2.
Thus, the net force accelerates the puck in the positive direction of the x axis.
Situation C: In Fig. 5-3f, force →F3 is not directed along the direction oof the puck.s acceleration, only x component F3,x is. (Force →F3 is two-dimensional but the motion is only one-dimensional.) Thus, we write Eq. 5-4 as

Figure 5-3 In three situations, forces act on a puck that moves along an x axis. Free-body diagrams are also shown.
F3,x−F2=max. (5−5)
From the figure, we see that F3,x=F3cosθ. Solving for the acceleration and substituting for F3,x yield
ax=F3,x−F2m=F3cosθ−F2m
=(1.0N)(cos30∘)−2.0N0.20kg=−5.7 m/s2.
Thus, the net force accelerates the puck in the negative direction of the x axis.
Topper's Solved these Questions
- FORCE AND MOTION - I BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - CHECKPOINT
5 Videos
- FORCE AND MOTION - I BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PROBLEMS
52 Videos
- FLUIDSBOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PRACTICE QUESTIONS (Integer Type )
5 Videos
- FORCE AND MOTION-IIBOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)
1 Videos
Similar Questions
Two horizontal forces →F1 and →F2 act on a 4.0 kg disk that slides over frictionless ice, on which an xy coordinate system over frictionless ice, on which an xy coordinate system is laid out. Force →F1 is in the positive direction of the x axis and has a magnitude of 7.0 N. Force →F2 has a magnitude of 9.0 N. Figure 5-39 gives the x component vx of the velocity of the disk as a function of time t during the sliding. What is the angle between the constant directions of forces →F1 and →F2 ?
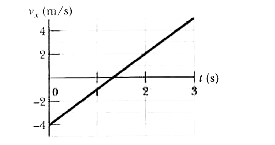
View SolutionTwo forces →F1=3ˆi+4ˆj and →F2=3ˆj+4ˆk are acting simultaneously at a point. What is the magnitude of the resultant force ?
View Solution
Knowledge Check
Two forces −→F1and−→F2 are acting at right angles to each other , find their resultant ?
A√F21−F22B√F21+F22C√(F1+F2)DF1+F2When force →F1,→F2,→F3 are acting on a particle of mass m, the particle remains in equilibrium. If the force →F1 is now removed then the acceleration of the particle is :
A→F1/mB→F1/mC→F2−→F3/mD→F2/mA force F=−kx3 is acting on a block moving along x-axis. Here, k is a positive constant. Work done by this force is
Apositive in displacing the block from x = 3 to x = 1Bpositive in displacing the block from x = - 1 to x = - 3Cnegative in displacing the block from x = 3 to x = 1Dnegative in displacing the block from x = - 1 to x = - 3
A force F=−kx3 is acting on a block moving along x-axis. Here, k is a positive constant. Work done by this force is
View SolutionA force F=α+βx acts on a particle of mass m along the X . Axis . Here αandβ are constants . Find the work done by this force when particle moves form x = 0 to x = d .
View SolutionA smooth track is in the form of a quarter circle of radius 10 m lies in the vertical plane. A bead moves from A and B along the circular track under the action of forces →F1,→F2 and →F3 Force →F1 acts always towards point B and is always 20 N in magnitude Force →F2 always acts horizontally and is always 25 N in magnitude. Force →F3 always acts tangentially to the track and is of constant magnitude 10 N. Select the correct answer.

View SolutionA smooth track in the form of a quarter circle of radius 6m lies in the vertical plane. A particle moves from P1 to P2 under the action of forces →F1,→F2 and →F3 Force →F1 is 20N, Force →F2 is always 30N in magnitude. Force →F3 always acts tangentiallly to the track and is of magnitude 15N. Select the correct alternative (s) :
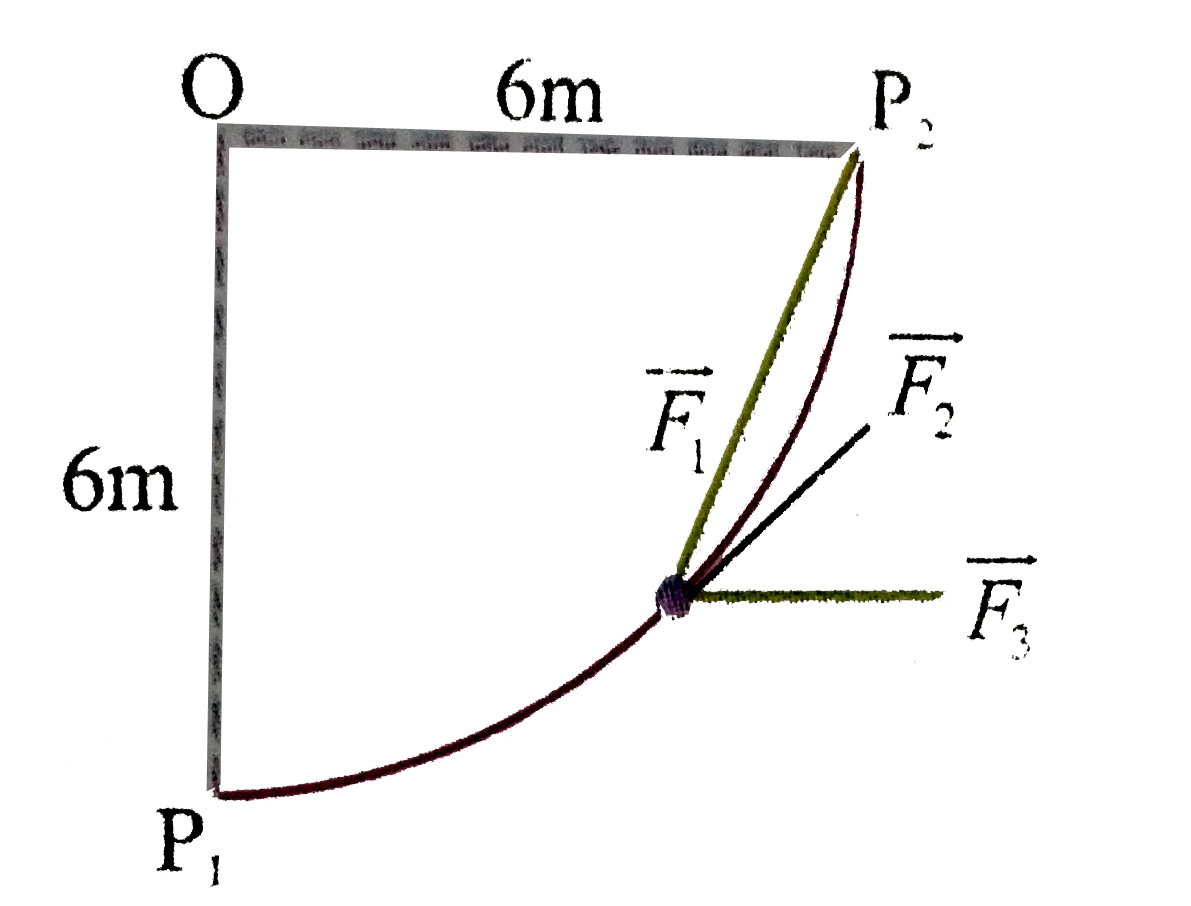 .
.
View SolutionA smooth track is in the form of a quarter circle of radius 10 m lies in the vertical plane. A bead moves from A and B along the circular track under the action of forces →F1,→F2 and →F3 Force →F1 acts always towards point B and is always 20 N in magnitude Force →F2 always acts horizontally and is always 25 N in magnitude. Force →F3 always acts tangentially to the track and is of constant magnitude 10 N. Select the correct answer.

View Solution
