Two horizontal forces act on a 2.5 kg chopping block that can slide over a frictionless kitchen counter, which lies in an xy plane. One force is →F1=(3.0 N)ˆi+(4.0N)ˆj. Find the acceleration of the chopping block in unit-vector notation when the other force is (a) →F2=(−3.0N)ˆi+(−4.0N)ˆj, (b) →F2=(−3.0N)ˆi+(4.0N)ˆj, and (c) →F2=(3.0N)ˆi+(−4.0N)ˆj.
To solve the problem step by step, we will analyze the forces acting on the chopping block and calculate the acceleration for each case.
Given:
- Mass of the chopping block, m=2.5kg
- Force →F1=(3.0N)^i+(4.0N)^j
(a) When →F2=(−3.0N)^i+(−4.0N)^j
1. Calculate the Net Force:
→Fnet=→F1+→F2=(3.0^i+4.0^j)+(−3.0^i−4.0^j)
→Fnet=(3.0−3.0)^i+(4.0−4.0)^j=0^i+0^j=0
2. Calculate the Acceleration:
→a=→Fnetm=02.5=0m/s2
(b) When →F2=(−3.0N)^i+(4.0N)^j
1. Calculate the Net Force:
→Fnet=→F1+→F2=(3.0^i+4.0^j)+(−3.0^i+4.0^j)
→Fnet=(3.0−3.0)^i+(4.0+4.0)^j=0^i+8.0^j=8.0^j
2. Calculate the Acceleration:
→a=→Fnetm=8.0^j2.5=3.2^jm/s2
(c) When →F2=(3.0N)^i+(−4.0N)^j
1. Calculate the Net Force:
→Fnet=→F1+→F2=(3.0^i+4.0^j)+(3.0^i−4.0^j)
→Fnet=(3.0+3.0)^i+(4.0−4.0)^j=6.0^i+0^j=6.0^i
2. Calculate the Acceleration:
→a=→Fnetm=6.0^i2.5=2.4^im/s2
Summary of Results:
- (a) →a=0m/s2
- (b) →a=3.2^jm/s2
- (c) →a=2.4^im/s2
- Mass of the chopping block, m=2.5kg
- Force →F1=(3.0N)^i+(4.0N)^j
→Fnet=→F1+→F2=(3.0^i+4.0^j)+(−3.0^i−4.0^j)
→Fnet=(3.0−3.0)^i+(4.0−4.0)^j=0^i+0^j=0
→a=→Fnetm=02.5=0m/s2
→Fnet=→F1+→F2=(3.0^i+4.0^j)+(−3.0^i+4.0^j)
→Fnet=(3.0−3.0)^i+(4.0+4.0)^j=0^i+8.0^j=8.0^j
→a=→Fnetm=8.0^j2.5=3.2^jm/s2
→Fnet=→F1+→F2=(3.0^i+4.0^j)+(3.0^i−4.0^j)
→Fnet=(3.0+3.0)^i+(4.0−4.0)^j=6.0^i+0^j=6.0^i
→a=→Fnetm=6.0^i2.5=2.4^im/s2
- (a) →a=0m/s2
- (b) →a=3.2^jm/s2
- (c) →a=2.4^im/s2
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)36videos
FORCE AND MOTION - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type)5videos
FORCE AND MOTION - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - CHECKPOINT5videos
FORCE AND MOTION - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PRACTICE QUESTIONS (Integer Type )5videos
FLUIDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)1videos
FORCE AND MOTION-II
Similar Questions
In unit vector notation, find the net torque about the origin on a particle located at (2.0m,−2.0m,−6.0m) when the three forces →F1=(6.0N)ˆj,→F2=(1.0N)ˆi−(2.0N)ˆj,and→F3=(4.0N)ˆi+(2.0N)ˆj−(3.0N)k act on the particle.
View SolutionA 1.50kg object is subjected to three forces that give it an acceleration →a=−(8.00m/s2)ˆj. If two of the three forces are →F1=(30.0N)ˆi+(16.0N)ˆj and −→F2=−(12.0N)ˆi+(8.00N)ˆj, find the third force.
View Solution
Knowledge Check
- Question 1 - Select One
A body is moving under the action of two force −→F1=2ˆi−5ˆj , −→F2=3ˆi−4ˆj . It's velocity will become uniform under a third force −→F3 given by.
A5ˆi−ˆjB−5ˆi−ˆjC5ˆi+ˆjD−5ˆi+9ˆj - Question 2 - Select One
A force →F=(ˆi+3ˆj)N acts on a body at a point P , which is at a distance , give by →r=(3ˆi+ˆj) m form the axis of rotation .
What is the direction of the torque acting on the body ?APositive X axisBPositive Y axisCPositive Z axisDNegative Z axis - Question 3 - Select One
Given →A=0.3ˆi+0.4ˆj+cˆk calculate the value of c if A is a unit vector.
A0.866B0.166C0.18D0.0866
A particle is to move along a line at the constant velocity →v=(2m/s)ˆi−(3m/s)ˆj. During the motion of the particle, we assume that two forces are acting on it. If one of the forces is →F=(2N)ˆi+(−5N)ˆj, find the other force.
View SolutionFind unit vector parallel to the resultant of the vectors →A=ˆi+4ˆj+2ˆk and →B=3ˆi−5ˆj+ˆk.
View SolutionTwo forces →F1=3ˆi+4ˆj and →F2=3ˆj+4ˆk are acting simultaneously at a point. What is the magnitude of the resultant force ?
View SolutionFind the area of the triangle formed by the tips of the vectors →a=ˆi−ˆj−3ˆk,→b=4ˆi−3ˆj+ˆk and →c=3ˆi−ˆj+2ˆk.
View SolutionTwo horizontal forces →F1 and →F2 act on a 4.0 kg disk that slides over frictionless ice, on which an xy coordinate system over frictionless ice, on which an xy coordinate system is laid out. Force →F1 is in the positive direction of the x axis and has a magnitude of 7.0 N. Force →F2 has a magnitude of 9.0 N. Figure 5-39 gives the x component vx of the velocity of the disk as a function of time t during the sliding. What is the angle between the constant directions of forces →F1 and →F2 ?
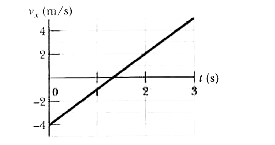 View Solution
View Solution

