In Fig. 25-7a switch S is closed to connect the uncharged capacitor of capacitance C =0.25μF to the battery of potential difference V=12V. The lower capacitor plate has thickness L=0.50 cm and face area A=2.0×10−4m2 and it consists of copper in which the density of conduction electrons is n=8.49×1025 electrons/m3. From what depth d within the plate (Fig.25-7b) must electrons move to the plate face as the capacitor becomes charged?
To solve the problem, we need to find the depth d within the copper plate from which electrons must move to the plate face as the capacitor becomes charged. We will follow these steps:
Step 1: Calculate the charge Q on the capacitor
The charge Q on a capacitor is given by the formula:
Q=C⋅V
Where:
- C=0.25μF=0.25×10−6F
- V=12V
Substituting the values:
Q=0.25×10−6F×12V=3.0×10−6C
Step 2: Calculate the number of electrons ne required to create this charge
The charge of a single electron e is approximately:
e=1.6×10−19C
The number of electrons ne can be calculated using:
ne=Qe
Substituting the values:
ne=3.0×10−6C1.6×10−19C≈1.875×1013electrons
Step 3: Calculate the volume Vd of copper required to provide these electrons
The volume of copper Vd that contains ne electrons can be calculated using the electron density n:
n=8.49×1025electrons/m3
The volume is given by:
Vd=nen
Substituting the values:
Vd=1.875×10138.49×1025≈2.21×10−13m3
Step 4: Relate the volume to the depth d
The volume of the copper plate can also be expressed in terms of the area A and the depth d:
Vd=A⋅d
Where:
- A=2.0×10−4m2
Rearranging for d:
d=VdA
Substituting the values:
d=2.21×10−13m32.0×10−4m2≈1.105×10−9m=1.105nm
Final Answer
The depth d from which electrons must move to the plate face as the capacitor becomes charged is approximately:
d≈1.1nm
The charge Q on a capacitor is given by the formula:
Q=C⋅V
Where:
- C=0.25μF=0.25×10−6F
- V=12V
Q=0.25×10−6F×12V=3.0×10−6C
The charge of a single electron e is approximately:
e=1.6×10−19C
The number of electrons ne can be calculated using:
ne=Qe
Substituting the values:
ne=3.0×10−6C1.6×10−19C≈1.875×1013electrons
The volume of copper Vd that contains ne electrons can be calculated using the electron density n:
n=8.49×1025electrons/m3
The volume is given by:
Vd=nen
Substituting the values:
Vd=1.875×10138.49×1025≈2.21×10−13m3
The volume of the copper plate can also be expressed in terms of the area A and the depth d:
Vd=A⋅d
Where:
- A=2.0×10−4m2
d=VdA
Substituting the values:
d=2.21×10−13m32.0×10−4m2≈1.105×10−9m=1.105nm
The depth d from which electrons must move to the plate face as the capacitor becomes charged is approximately:
d≈1.1nm
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - CHECKPOINTS4videos
CAPACITANCE
- BOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PROBLEMS48videos
CAPACITANCE
- BOOK - RESNICK AND HALLIDAYCHAPTER - ALL ABOUT ATOMS EXERCISE - CHECKPOINT1videos
ALL ABOUT ATOMS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Integer )4videos
CENTER OF MASS
Similar Questions
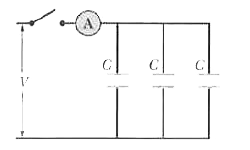
Each of the uncharged capacitors in Fig 25-34 has a capacitance of 25.0μF. A potential difference of V=750 V is established when the switch is closed . How many coulombs of charge then pass through meter A?
 View Solution
View SolutionA capacitor of capacitance C is connected to a 6.0V battery through a resistance of 5Ω .The potential difference between the plates rises from zero to 3.0V in 6.9μS.The value of C
View Solution
Knowledge Check
- Question 1 - Select One
A parallel plate capacitor has capacitance of 1.0F. If the plates are 1.0mm apart, what is the area of the plates?
A1.1×105m2B2.1×108m2C0.5×108m2D1.6×108m2 - Question 2 - Select One
An uncharged capacitor of capacitance 4μf, a battery of emf 12 volt and a resistor of 2.5MΩ are connected in series. The time after which vC=3vRis(take ln2=0.693)
A6.93secB13.86secC20.52secDnone of these - Question 3 - Select One
In the circuit shown in fig, switch S was closed for long time. At time t-0, teh switch is opened again. The maximum potential difference across teh plates of the capacitor after the switch is opened is
 A10VB100VC20VD200V
A10VB100VC20VD200V
In Fig 25-33 the battery has a potential difference of V=12.0 V and the five capacitors each have a capacitance each have a capacitance of 10.0μF What is the charge on (a) capacitor 1 and (b) capacitor 2?
 View Solution
View SolutionA capacitor has a capacitance of 7.28μF. What amount of charge must be placed on each of its plates to make the potential difference between its plates equAl to 25.0V?
View SolutionA parallel plate capacitor has capacitance of 1.0F. If the plates are 1.0mm apart, what is the area of the plates?
View SolutionEstimate the average drift velocity of conduction electrons in a copper wire of cross-sectional area 2.5×10−7m2, carrying a current of 2.7 A. Assume the density of conduction electrons to be 9×1028m−3.
View SolutionTwo capacitor in Fig 25-37 has a capacitance of 30μF and is initially uncharged. The battery provides a potential difference of 120 V. After switch S is closed, how much charge will pass through it?
 View Solution
View Solution

