A 2.0μF capacitor and a 4.0μF, capacitor are connected in parallel across in 300V potential difference (a) What is the total energy stored by them? (b) They are next connected in series across that potential difference. What is the ratio of the total energy stored by them in the parallel arrangement to that in the series arrangement?
To solve the problem step by step, we will calculate the total energy stored in the capacitors when they are connected in parallel and then when they are connected in series. Finally, we will find the ratio of the energies stored in both arrangements.
Step 1: Calculate Total Capacitance in Parallel
When capacitors are connected in parallel, the total capacitance (C_total) is the sum of the individual capacitances.
Ctotal=C1+C2=2.0μF+4.0μF=6.0μF
Step 2: Calculate Energy Stored in Parallel
The energy (U) stored in a capacitor is given by the formula:
U=12CV2
Where:
- C is the capacitance in farads (F)
- V is the voltage in volts (V)
Substituting the values for the parallel arrangement:
Uparallel=12×6.0×10−6F×(300V)2
Calculating this:
Uparallel=12×6.0×10−6×90000
Uparallel=0.27J
Step 3: Calculate Total Capacitance in Series
When capacitors are connected in series, the total capacitance (C_total) is given by:
1Ctotal=1C1+1C2
Substituting the values:
1Ctotal=12.0μF+14.0μF
Calculating this:
1Ctotal=12+14=24+14=34
Thus,
Ctotal=43μF
Step 4: Calculate Energy Stored in Series
Using the same energy formula for the series arrangement:
Useries=12CtotalV2
Substituting the values:
Useries=12×43×10−6F×(300V)2
Calculating this:
Useries=12×43×10−6×90000
Useries=23×0.06=0.06J
Step 5: Calculate the Ratio of Energies
Now, we find the ratio of the total energy stored in the parallel arrangement to that in the series arrangement:
Ratio=UparallelUseries=0.27J0.06J=4.5
Final Answers:
(a) The total energy stored by the capacitors in parallel is 0.27 J.
(b) The ratio of the total energy stored in the parallel arrangement to that in the series arrangement is 4.5.
When capacitors are connected in parallel, the total capacitance (C_total) is the sum of the individual capacitances.
The energy (U) stored in a capacitor is given by the formula:
- C is the capacitance in farads (F)
- V is the voltage in volts (V)
Uparallel=0.27J
When capacitors are connected in series, the total capacitance (C_total) is given by:
Using the same energy formula for the series arrangement:
Useries=23×0.06=0.06J
Now, we find the ratio of the total energy stored in the parallel arrangement to that in the series arrangement:
(a) The total energy stored by the capacitors in parallel is 0.27 J.
(b) The ratio of the total energy stored in the parallel arrangement to that in the series arrangement is 4.5.
Topper's Solved these Questions
- CAPACITANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
23 Videos
- CAPACITANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
12 Videos
- CAPACITANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - CHECKPOINTS
4 Videos
- ALL ABOUT ATOMS BOOK - RESNICK AND HALLIDAYCHAPTER - ALL ABOUT ATOMS EXERCISE - CHECKPOINT
1 Videos
- CENTER OF MASS BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Integer )
4 Videos
Similar Questions
N identical capacitors are connected in parallel which are charged to a potential V. If these are separated and connected in series then what potential difference will be obtained?
View SolutionThree capacitors having capacitances of 8.4μF,8.2μF and 4.21μF are connected in series across a 36 potential difference.
(a) What is the charge on 4.2μF capacitor?
(b) What is the total energy stored in all three capacitors?
(c) The capacitors are disconnected from the potential difference without allowing them to discharge. They are then reconnected in parallel with each other, with the positively charged plates connected together. What is the voltage across each capacitor in the parallel combination?
(d) What is the total energy now stored in the capacitors?
View Solution
Knowledge Check
A system of 2 capacitors of capacitance 2 μF and 4 μF is connected in series across a potential difference of 6 V. The electric charge and energy stored in the system are
A36μCand108μJB8μCand24μJC1μCand3μJD10μCand30μJTwo capacitors of 3μF and 6μF are connected in series and a potential difference of 900 V is applied across the combination. They are then disconnected and reconnected in parallel. The potential difference across the combination is
AZeroB100 VC200 VD400 VTwo capacitors 3μF and 6μF are connected in series across a potential difference of 120V. Then the potential difference across 3μF capacitor is:
A40VB60VC80VD100V
Two capacitors are connected in parallel and the energy stored is 18 J, when a potential difference of 6000 V is applied across the combination. With the same capacitors connected in series, the energy stored is 4 J from the same potential difference. what are the individual capacitances?
View SolutionA 5 μF capacitor is connected in series with a 10 μF capacitor. When a 300 Volt potential difference is applied across this combination, the energy stored in the capacitors is
View SolutionIn the circuit shown in the figure, the potential difference across the 4.5μF capacitor is
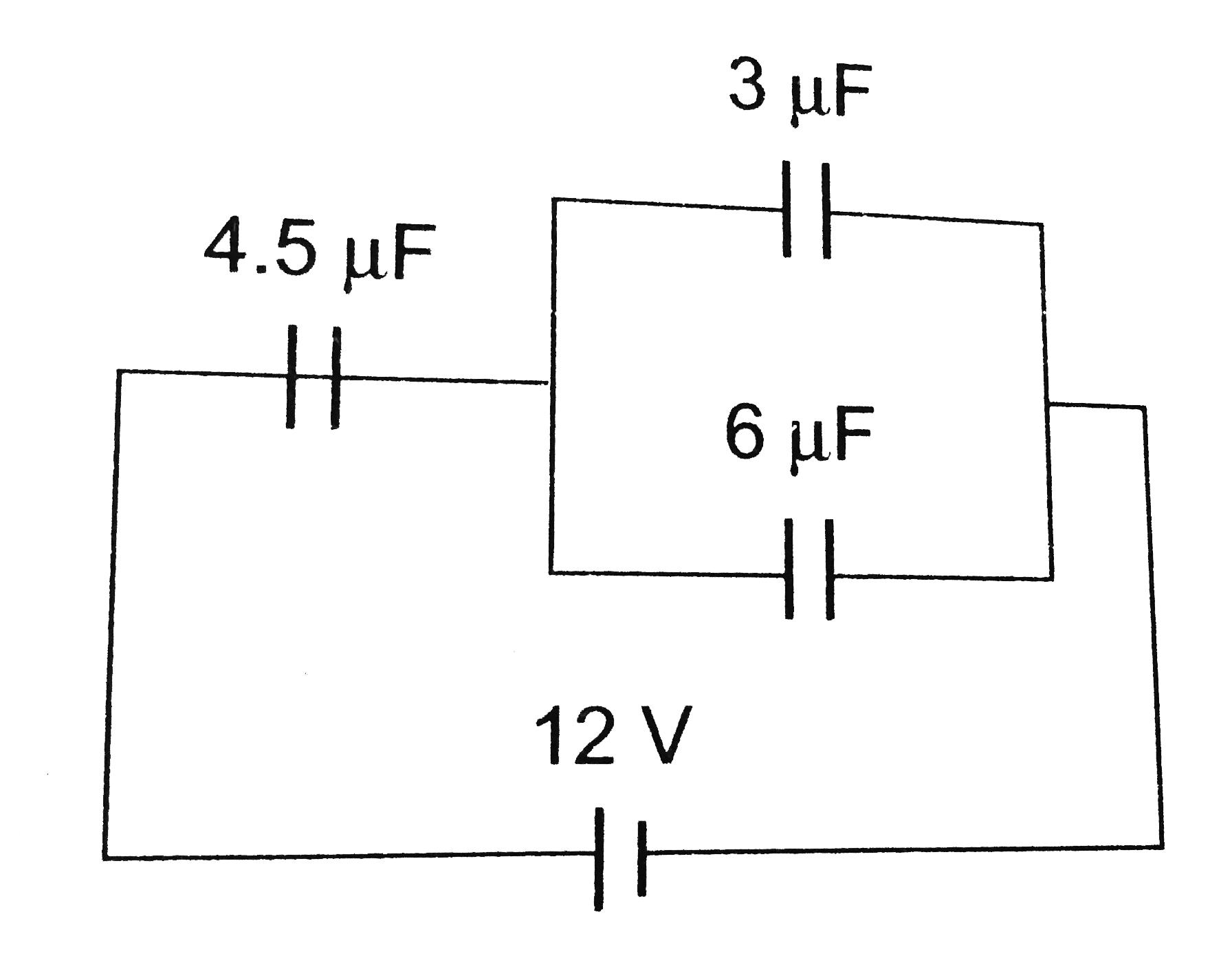
View SolutionHow many 1μF capacitors must be connected in parallel to store a charge of 1 C with a potential of 110 V across the capacitors?
View SolutionFour capacitors 4μF,6μF,5μF,3μF are connected in series to a source of 150V. The potential difference in volt, the 5μF capacitor will be
View Solution
