What flows through a garden hose at a volume flow rate dV/dt of 450cm3/s. What
The current I of negative charge is due to the electrons in the water molecules moving through the hose. The current is the rate at which that negative charge passes through any plane that cuts completely across the hose.
Calculations: Calculations: We can write the current in terms of the number of molecules that pass through such a plane per second as
i=(charge per electron) (electrons per molecule) (molecules per second)
or i=(e)(10)dNdt
We substitute 10 electrons per molecule because a water (H2O) molecule contains 8 electrons in the single oxygen atom and 1 electron in each of the two hydrogen atoms.
We can express the rate dN/dt in terms of the given volume flow rate dV/dt by first writing (molecule per second)=(molecules per mole) (moles per unit mass)
×(mass per unit volume)(volume per second)
"Molecules per mole" is Avogadro.s number NA. "Moles per unit mass" is the inverse of the mass per mole, which is the molar mass M of water. "Mass per unit volume" is the (mass) density pmass of water. The volume per second is the volume flow rate dV/dt. Thus, we have dNdt=NA(1M)pmass(dVdt)=NApmassMdVdt
Substituting this into the equation for i, we find
i=10eNAM−1pmassdVdt
We know that Avogadro.s number NA. is 6.02×1023 molecules/mol, or 6.02×1023 mol−1, and from Table 15-1 we know that the density of water pmass pris under normal conditions is 1000 kg/m3. We can get the molar mass of water from the molar masses listed in Appendix F (in grams per mole): We add the molar mass of oxygen (16 g/mol) to twice the molar mass of hydrogen (1 g/mol), obtaining 18 g/mol = 0.018 kg/mol. So, the current of negative charge due to the electrons in the water is
i=(10)(1.6×10−19C)(6.02×1023mol−1)×(0.018kg/mol)−1(1000kg/m3)(450×10−6m3/s)
=2.41×107C/s=2.41×107A
=24.1MA.
This current of negative charge is exactly compensated by a current of positive charge associated with the nuclei of the three atoms that make up the water molecule. Thus, there is no net flow of charge through the hose.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - CURRENT AND RESISTANCEEXERCISE - Checkpoints6videos
CURRENT AND RESISTANCE
- BOOK - RESNICK AND HALLIDAYCHAPTER - CURRENT AND RESISTANCEEXERCISE - Problems36videos
CURRENT AND RESISTANCE
- BOOK - RESNICK AND HALLIDAYCHAPTER - CIRCULAR MOTIONEXERCISE - CHECK POINTS6videos
CIRCULAR MOTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELASTICITYEXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
ELASTICITY
Similar Questions
An ideal fluid flows through a pipe of circular cross section of radius r at a speed v0. Now a viscous liquid is made to flow through the pipe at the same volume flow rate (measured in m3s–1). Find the maximum speed of a fluid particle in the pipe.
View SolutionA "flow calorimeter" is used to measure the specific heat of a liquid. Heat is added at a known rate to a stream of the liquid as it passes through the calorimeter at known rate, then a measurement of the resulting temperature difference between the in flow and the out flow points of the liquid stream enables us to compute the specific heat of the liquid. A liquid of density 0.85 g/cm3 flows through a calorimeter at the rate of 8.0 cm3/s. heat is added by means of a 250 watt electric heating coil, and a temperature difference of 15∘C is established in steady state conditions between the in flow and out flow points.
Q. Rate of heat absorption per unit specific heat capacity isView Solution
Knowledge Check
- Question 1 - Select One
A "flow calorimeter" is used to measure the specific heat of a liquid. Heat is added at a known rate to a stream of the liquid as it passes through the calorimeter at known rate, then a measurement of the resulting temperature difference between the in flow and the out flow points of the liquid stream enables us to compute the specific heat of the liquid. A liquid of density 0.85 g/cm3 flows through a calorimeter at the rate of 8.0 cm3/s. heat is added by means of a 250 watt electric heating coil, and a temperature difference of 15∘C is established in steady state conditions between the in flow and out flow points.
Q. Rate of heat absorption per unit specific heat capacity isA100g-.∘C/sB102g-.∘C/sC50g-.∘C/sD10.2g−.∘C/s - Question 2 - Select One
A "flow calorimeter" is used to measure the specific heat of a liquid. Heat is added at a known rate to a stream of the liquid as it passes through the calorimeter at known rate, then a measurement of the resulting temperature difference between the in flow and the out flow points of the liquid stream enables us to compute the specific heat of the liquid. A liquid of density 0.85 g/cm3 flows through a calorimeter at the rate of 8.0 cm3/s. heat is added by means of a 250 watt electric heating coil, and a temperature difference of 15∘C is established in steady state conditions between the in flow and out flow points.
Q. Rate of heat added per second isA4.18 J/sB59.8 cal/sC5 cal/sD90 cal/2 - Question 3 - Select One
A "flow calorimeter" is used to measure the specific heat of a liquid. Heat is added at a known rate to a stream of the liquid as it passes through the calorimeter at known rate, then a measurement of the resulting temperature difference between the in flow and the out flow points of the liquid stream enables us to compute the specific heat of the liquid. A liquid of density 0.85 g/cm3 flows through a calorimeter at the rate of 8.0 cm3/s. heat is added by means of a 250 watt electric heating coil, and a temperature difference of 15∘C is established in steady state conditions between the in flow and out flow points.
Q. Specific heat of the liquid isA0.59cal/g.∘CB4cal/g.∘CC2cal/g.∘CD9cal/g.∘C
A "flow calorimeter" is used to measure the specific heat of a liquid. Heat is added at a known rate to a stream of the liquid as it passes through the calorimeter at known rate, then a measurement of the resulting temperature difference between the in flow and the out flow points of the liquid stream enables us to compute the specific heat of the liquid. A liquid of density 0.85 g/cm3 flows through a calorimeter at the rate of 8.0 cm3/s. heat is added by means of a 250 watt electric heating coil, and a temperature difference of 15∘C is established in steady state conditions between the in flow and out flow points.
Q. Rate of heat added per second isView SolutionA "flow calorimeter" is used to measure the specific heat of a liquid. Heat is added at a known rate to a stream of the liquid as it passes through the calorimeter at known rate, then a measurement of the resulting temperature difference between the in flow and the out flow points of the liquid stream enables us to compute the specific heat of the liquid. A liquid of density 0.85 g/cm3 flows through a calorimeter at the rate of 8.0 cm3/s. heat is added by means of a 250 watt electric heating coil, and a temperature difference of 15∘C is established in steady state conditions between the in flow and out flow points.
Q. Specific heat of the liquid isView SolutionWater flows through a horizontal pipe of radius 1 cm at a speed of 8 cm s−1. What will be the speed of flow of water under similar conditions, if the radius of the pipe is doubled ?
View SolutionThe figure shows a pipe and gives the volume flow rate (in cm3/s) and the direction of flow for all but one section . What are the volume flow rate and the direction of flow for that section ?
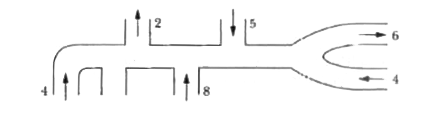 View Solution
View SolutionWater flows through a horizontal pipe of radius 1 cm at a speed of 8 cm s−1. What will be the speed of flow of water under similar conditions, if the radius of the pipe is doubled ?
View Solution

