As a car rolls along pavement, electrons move from the pavement first onto the tires and then onto the car body. The car stores this excess charge and the associated electric potential energy as if the car body were onc plate of a capacitor and the pavement were the olher plate (Fig. 27-35a). When the car stops, it discharges its excess charge and energy through the tires, just as a capacitor can discharge through a resistor. If a conducting object comes within a few centimeters of the car before the car is discharged, the remaining energy can be suddenly transferred to a spark between the car and the object. Suppose the conducting object is a fuel dispenser. The spark will not ignite the fuel and cause a fire if the spark energy is less than the critical Value Ufire=50mJ.
When the car of Fig. 27-35a stops at time t=0, the car ground potential difference is V0=30kV. The car-ground capacitance is C=500pF, and the resistance of each tire is Rtire=100GΩ. How much time does the car take to discharge through the tires to drop below the critical value Ufire?
(1) At any time t, a capacitor.s stored electric potential energy U is related to its stored charge d according to Eq. 25-21 (U=q2/2C) While a capacitor is discharging, the charge decreases with time according to Eq. 27-49 q=q0e−1/RC
Calculations. We can treat the times as resistors that are connected to one another at their tops via the car body and at their bottoms via the pavement. Figure 27-35b shows how the four resisters are connected in parallel across the car.s capacitance and Fig. 27-35c shows 
Figure 27-35 (a) A charged car and the pavement acts like a capacitor that can discharge through the tires (b) The effective circuit of the car-pavement capacitor, with four tire resistances Rtire connected in parallel. (c) The equivalent resistance R of the tires. (d) The electric potential energy U in the car-pavement capacitor decreases during discharge.
their equivalent resistance R. From Eq. 27-24, R is given by 1R=1Rtire+1Rtire+1Rtire+1Rtire
orR=Rtire4=100×109Ω4=25×109Ω.
When the car stops, it discharges its excess charge and energy through R. We now use our two Key Ideas to analyze the discharge Substituting Eq. 27-49 into Eq. 25-21 gives U=q22C=q0e−t/RC22C=q202Ce−2t/RC
From Eq. 25-1 (q= CV), we can relate the initial charge q0 on the car to the given initial potential difference V0:q0=CV0. Substituting this equation into Eq. 27-55 brings us to U=(CV0)22Ce−2t/RC=CV202e−2t/RC
ore−2t/RC=2UCV20.
Taking the natural logarithms of both sides, we obtain
−2tRC=ln(2U)CV20.
or t=−RC2ln(2U)CV20
Substituting the given data, we find that the time the car takes to discharge to the energy level Ufire=50 mJ is
t=(25×109Ω)(500×10−12F)2
×ln(2(50×10−3J))(500×10−12F)(30×103V)2
=9.4 s
Fire or no fire: This car requires at least 9.4 s before fuel can be brought safely near it. A pit crew cannot wait that long. So the tires include some type of conducting material (such as carbon black) to lower the tire resistance and thus increase the discharge rate, Figure 27-35d shows the stored energy U versus time t for tire resistances of R=100GΩ (our value) and R=10GΩ. Note how much more rapidly a car discharges to level Ufire with the lower R value.
Topper's Solved these Questions
- CIRCUITSBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Checkpoints
7 Videos
- CIRCUITSBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Problems
45 Videos
- CENTER OF MASS BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Integer )
4 Videos
- CIRCULAR MOTIONBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCULAR MOTIONEXERCISE - CHECK POINTS
6 Videos
Similar Questions
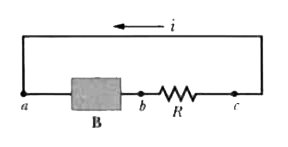
The figure shows the current I in a single-loop circuit with a battery B and a resistance R (and wires of negligible resistance). (a) Should the emf arrow at B be a drawn pointing leftward or rightward? At points a,b and c rank (b) the magnitude of the current )c the electric potential, and (d) the electric potential energy of the charge carriers greatest first.
View SolutionAn isolated charged capacitor may gradually discharge as charge leaks from one plate to the other through the intermediate material, as if it were discharging through an external resistor. (a) What is the resistance of such an external resistor if a 2.00μF capacitor's potential difference decreases to 60.0% of its initial value of 50.0 V in 2.40 d? (b) What is the corresponding loss of potential energy in that time interval? (c) At the end of that interval, at what rate is the capacitor losing potential energy?
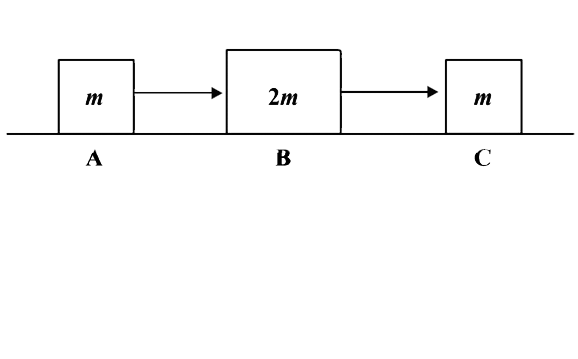
View SolutionThere object A,B and C are kept is a straing line a fritionlas horizental surface . These have masses have increase on 2m and m repectively . The object A move toward B with a speed 9 m//s and makes as electic collision with a there after B makes complately inclesis with C . All motion over on the same strangth line . Find the first speed of the object C
View SolutionA manufacturer of CD drives claims that the player can spin the disc as frequencly as 1200 revolutioins per minute. If the spinning is at this rate, what is the speed (in m/s) of the outer row of data on the disc, this row is located 5.6 cm from the center of the disc?
View SolutionConsider the situation given in (Fig. 5.71). Two cars are moving along road 1 and 2. Draw the direction of the motion of
(a) Car B as seen from car A.
(b) Car A as seen from car B.
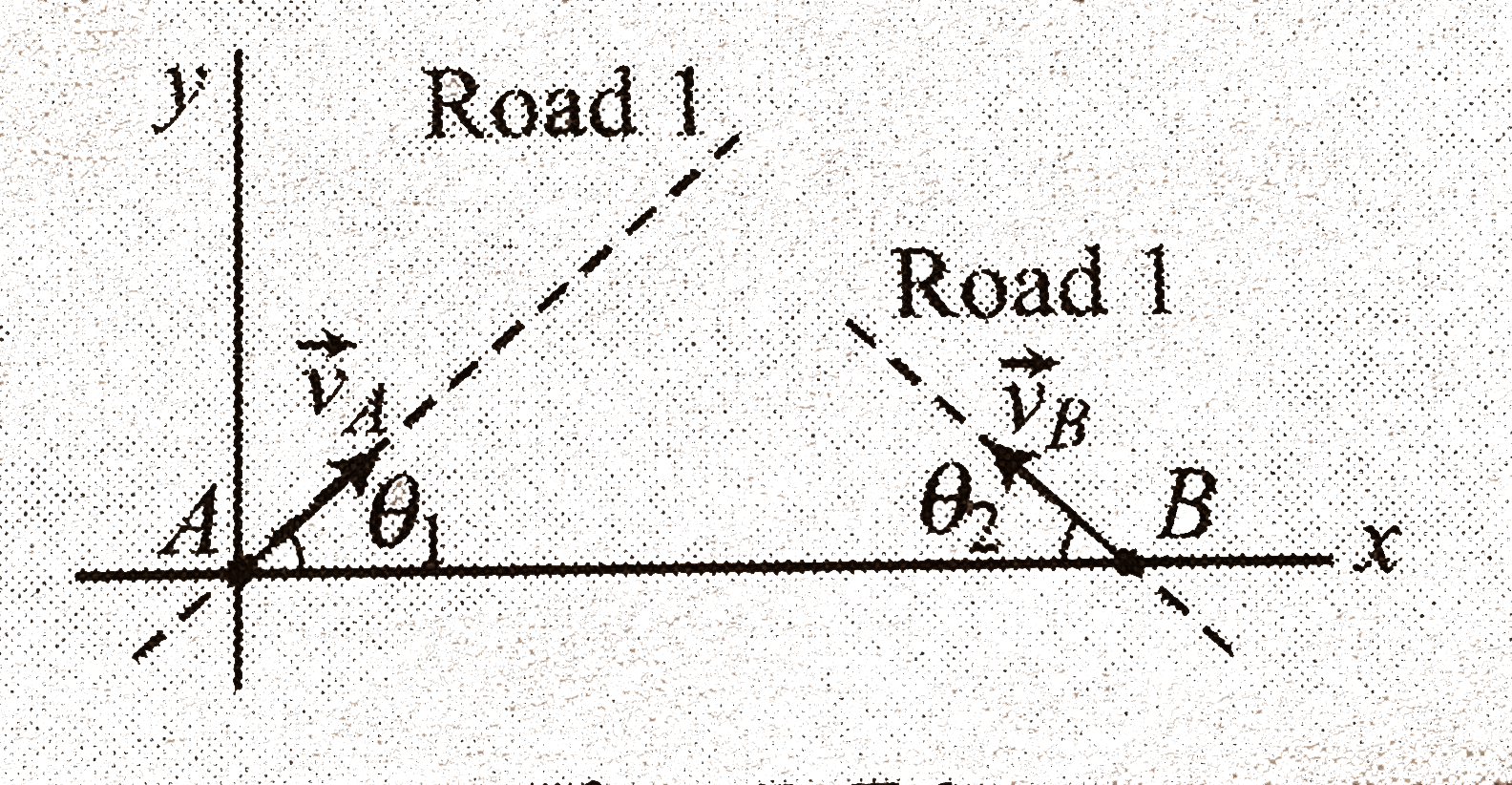 .
.
View SolutionA rolling body is connected with a trolley car by a spring of stiffness k . It does not slide and remains in equilibrium relative to the acceleration trolley car. If the trolly car is stopped after a time t=t_(0) . (the rolling body touches the trolly)
View SolutionA slowly moving flat car is 12.0 m long passing apoint at straight road at 10 kph. A boy beside the road near to that point tosses rocks onto the moving flat car at the rate of one per second, (a) If the first rock just hits the front edge of the car, how many rocks will fall on to that car ? (b) How many rocks will fall onto that car if the car begins to accelerate at 0.5m/s2, just as the first rock hits the car ?
View Solutionएक मोटर कार सीधी सड़क पर एकसमान चाल u से गतिमान है । सड़क तथा टायरों के बीच घर्षण गुणांक μ है । यदि कार का इंजन बन्द कर दिया जाये तो कार - (i) कितनी दूर जाकर, (ii) कितने समय बाद रुक जायेगी ?
View Solutionव्याख्या कीजिए कि कार को चलाते - चलाते उसके टायरों में वायुदाब बढ़ जाता हैं ।
View SolutionIn a system used for spraying cars, a car body is positively charged. Neutral droplets of paint are then attracted to the car because the positive car body induces a charge on the droplets of paint. Which diagram best shows the charge pattern?
View Solutionद्रव्यमान m की एक कार संवेग p से गति कर रही हैं | यदि कार के टायरों एवं सड़क के मध्य घर्षण नियतांक μ हैं तो केवल घर्षण के कारण कार द्वारा रुकने से पूर्व तय की गई दूरी होगी :
View Solutionएक ट्रक तथा कार समान गतिज ऊर्जा से गतिमान हैं । वे ब्रेकों द्वारा समान मंदन बल लगाकर रोके जाते हैं । ट्रक पहले रुकेगा या कार ।
View Solutionएक कार सीधी क्षैतिज रोड पर 'v0' वेग से गति कर रही है। यदि रोड तथा कार के टायरों के मध्य घर्षण गुणांक μ हो तो वह न्यूनतम दूरी ज्ञात करो जिसमें कार को ब्रेक लगाकर रोका जा सके।
View SolutionFill in the blanks: Car tires are produced with ______.
View Solutionশূন্যস্থান পূরণ করো : ______ দিয়েই তৈরি করা হয় গাড়ির টায়ার ।
View Solution
