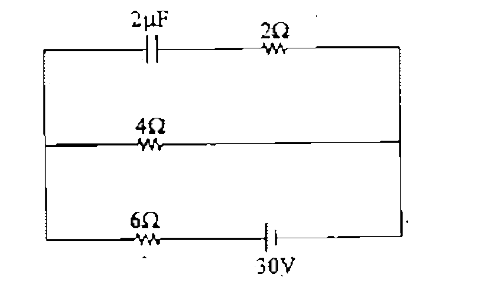
(a) Find the current I supplied by the battery in the network as shown in steady state. (b) Find the steady state charge on the capacitor. (c) Find the initial current through the battery.
Text Solution
Here we do not have a simple RC circuit as seen in Section 27.7. So, we cannot apply Eqs. 27-43 and 27-44 here. We have studied in Section 27.7 that an uncharged 
capacitor will intially behave like short circuit and after a long time behave lika a broken wire.
Calcualations (a) Once the capacitor is charged, no current will go through it and the current through the middle branch of the circuit is zero in steady state. The 4Ω resistor will have no current in it and may be omitted for current analysis. The 2Ωand6Ω resistors are therefore connected in series and hence i=2V2Ω+6Ω=0.25A
(B) The potential drop the across the 6Ω resistor is 6Ω=0.25A=1.5V. As there is no current in the 4Ω resistor there is no potential drop across it. The potential difference across the capacitor is, therefore, 1.5V. The charge on this capacitor is
Q=CV=2μF×1.5V=3μC
(c) At the initial moment, an uncharged capacitor can be assumed to be short circuited. So, the equivalent reisistance of the circuit will be 4.4Ω. The current through the battery will be 24.4A=0.45A
|
Topper's Solved these Questions
- CIRCUITSBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Checkpoints
7 Videos
- CIRCUITSBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Problems
45 Videos
- CENTER OF MASS BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Integer )
4 Videos
- CIRCULAR MOTIONBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCULAR MOTIONEXERCISE - CHECK POINTS
6 Videos
Similar Questions
Knowledge Check
Find the current supplied by the battery ?
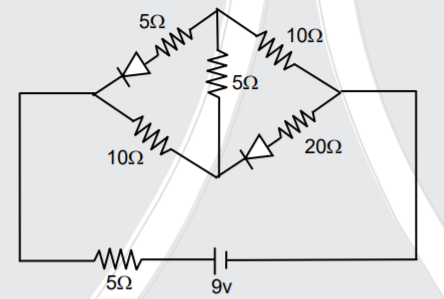 A0.1AB0.3AC0.4AD0.5A
A0.1AB0.3AC0.4AD0.5A
Find the steady state charge stored in the capacitor.
View Solution(a)Find the current I supplied by the battery in the network shown in figure in steady state. (b)find the charge on the capacitor.

View Solution(a)Find the current I supplied by the battery in the network shown in figure in steady state. (b)find the charge on the capacitor.

View SolutionFind the current supplied by the battery in the circuit shown in figure.

View SolutionFind the current supplied by the battery in the circuit shown in figure.

View SolutionFind the current supplied by the battery in the circuit shown in figure.

View SolutionFind the current supplied by the battery in the circuit shown in figure.
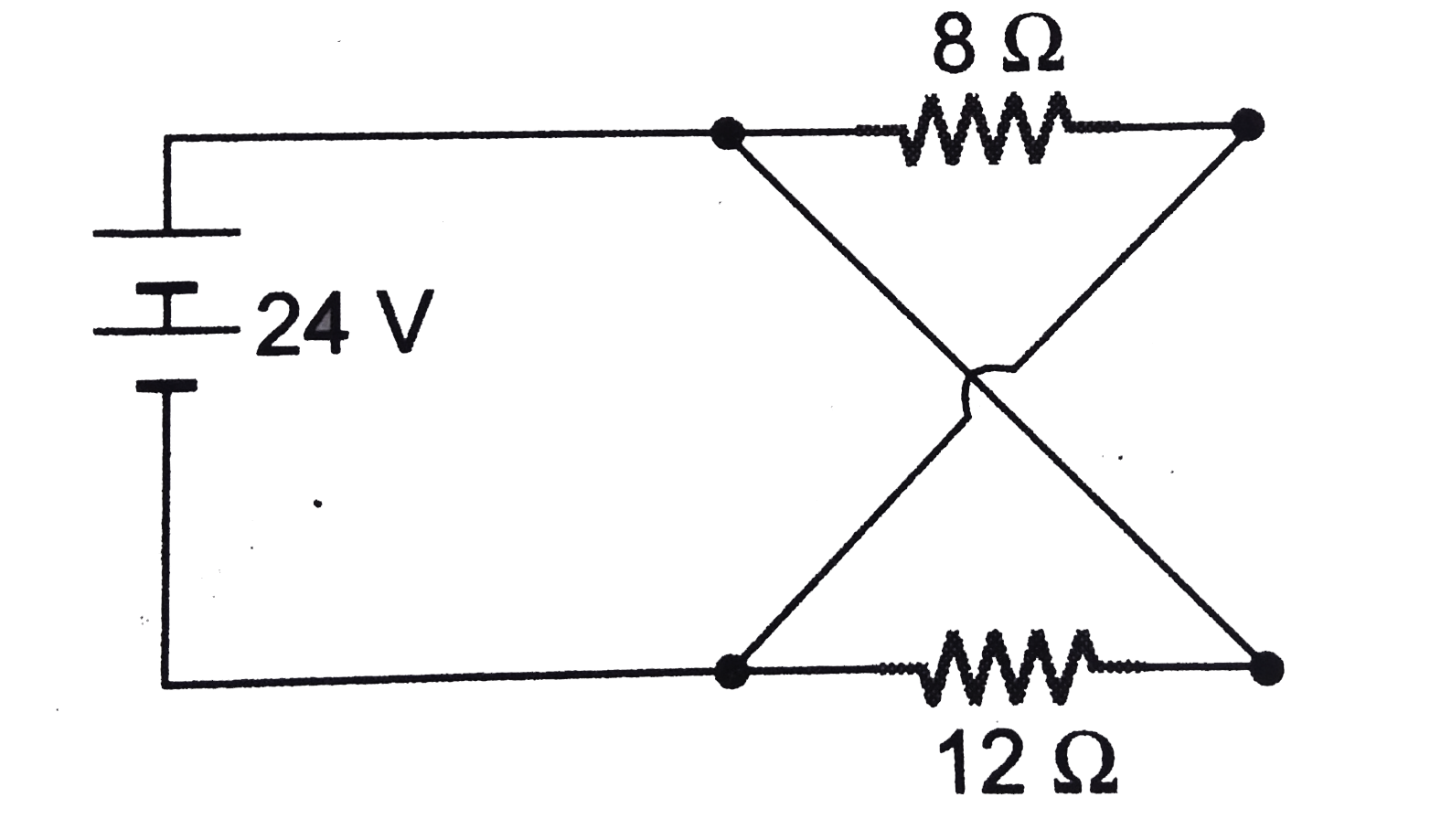
View Solution

